Предмет: Алгебра,
автор: Pavlik7739
СРОЧНО ПОЖАЛУЙСТА ПОМОГИТЕ!!!!!
Приложения:
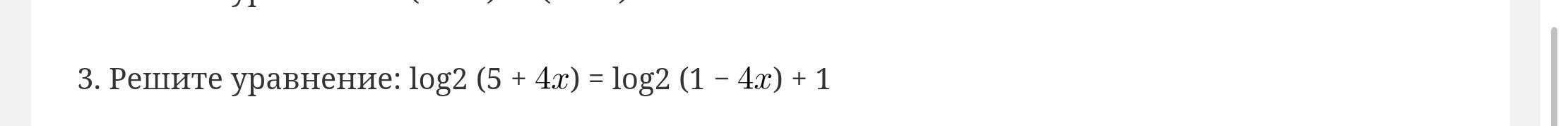
Ответы
Автор ответа:
1
Ответ:-0.25
Объяснение:
NNNLLL54:
ОДЗ не пишете, проверку не делаете...
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: катюшаборзенкова
Предмет: Другие предметы,
автор: dotadino
Предмет: Русский язык,
автор: tan123dem
Предмет: Физика,
автор: SavioKings
Предмет: Математика,
автор: марк277