Предмет: Математика,
автор: nguseva01
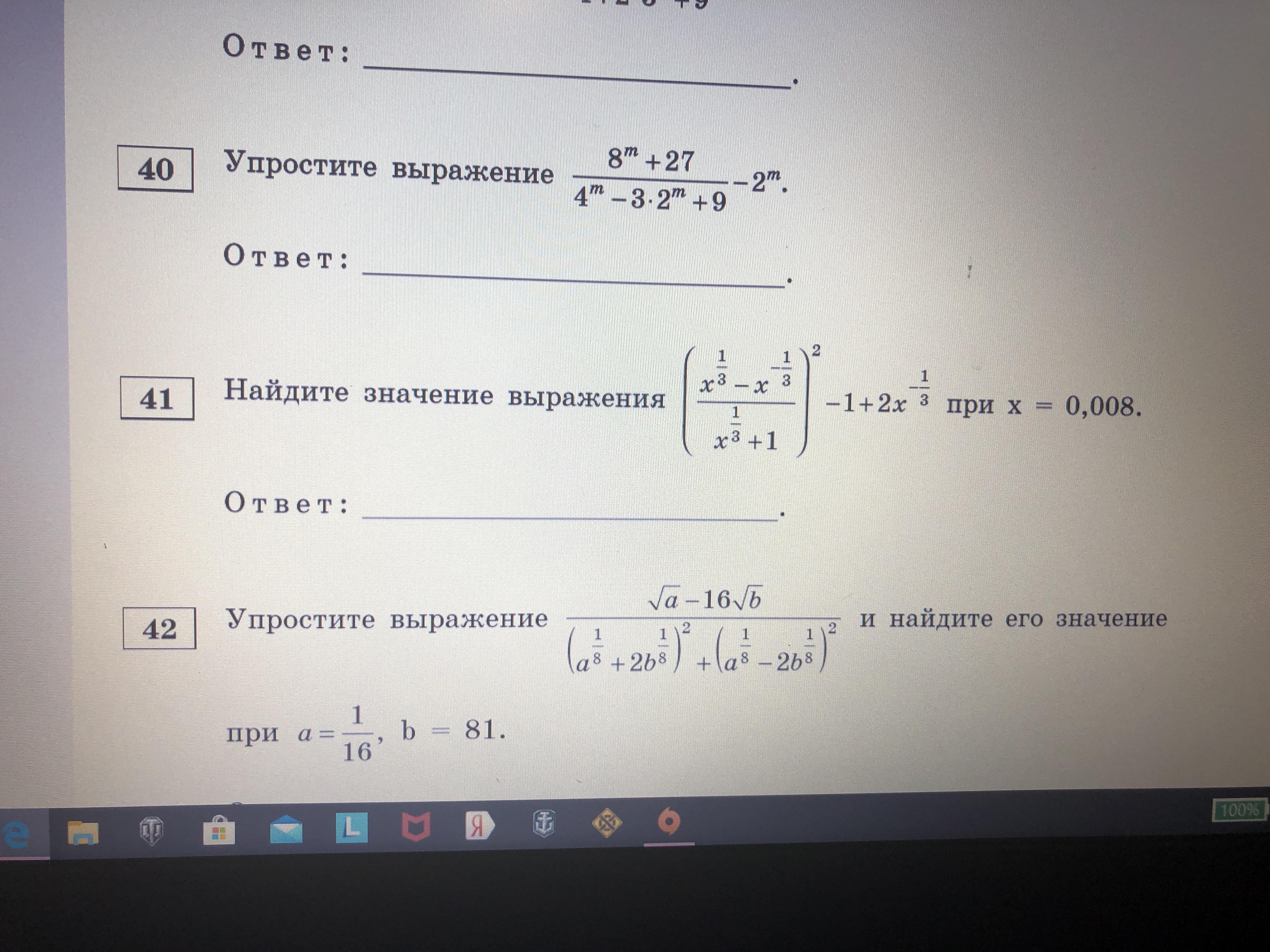
Решите 41 пожалуйста
Приложения:
Ответы
Автор ответа:
0
Ответ:
25
Пошаговое объяснение:
Обозначим для удобства :
Возвести положительное число в степень 1/3 — значит извлечь из него кубический корень.
Похожие вопросы
Предмет: Українська мова,
автор: Vana000
Предмет: Другие предметы,
автор: nataly8680
Предмет: Русский язык,
автор: arturminasyanарме
Предмет: Алгебра,
автор: raxilyashabano
Предмет: Алгебра,
автор: olgarebrakovaоля