Question

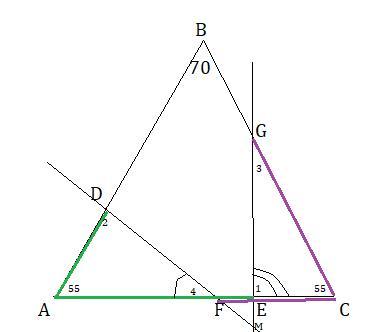
На основании равнобедренного треугольника отметили две различные точки F и E , а на боковых сторонах AB и –BC точки D и G соответственно так, что AD +AE = AC и CF+ CG = AC. Найти угол между прямыми DF и EG, если угол ABC = 70.

Answer 1

На основании равнобедренного треугольника отметили две различные точки F и E , а на боковых сторонах AB и –BC точки D и G соответственно так, что AD +AE = AC и CF+ CG = AC. Найти угол между прямыми DF и EG, если угол ABC = 70°.

Объяснение:

ΔАВС-равнобедренный,значит ∠А=∠В=(180°-70°):2=55°.

По условию АD+АЕ=АС и CF+ CG = AC ⇒АD=ЕС и AF=CG.

ΔADF ≈ΔCFG по 2 пропорциональным сторонам и равному углу между ними :∠А=∠В  и AD/EC=AF/CG ⇒соответственные углы равны ∠1=∠2 ,∠3=∠4.

ΔFEM  :  найдем угол ∠М  ;  ∠Е=∠1, ∠F=∠4 . Сумма углов ∠F+∠Е=180°-55°=125°  , тогда ∠М=180°-125°=55°