Предмет: Геометрия,
автор: Nurzhan94
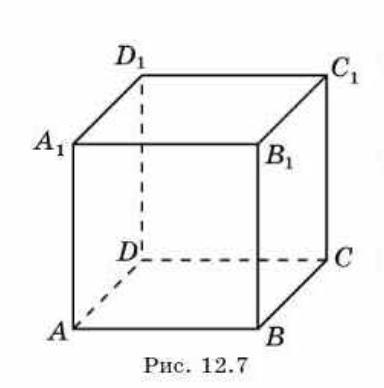
В единичном кубе abcda1b1c1d1 найдите расстояние от вершины А до плоскости a) ВСС1 b) BCD1
Приложения:
Аноним:
1) расстояние АВ. т.е. 1.
а во втором ?
2) находим диагональ куба. Д1В=√3. Проводим перпендикуляр к диагонали. По теореме Пифагора √(1²-(√3/2)²)=√(1-3/4)=√1/4=1/2.
Каждое расстояние, которое вы, ищите должно быть самым коротким. Т.е. перпендикуляром. К плоскости.
Ответы
Автор ответа:
54
Ответ:
a) 1 ; b)√2/2
Объяснение:
Так как длина ребра куба 1, а расстояние это перпендикуляр, то расстояние от точки A до плоскости BCC1, будет ребро AB длиной 1,во втором случае диагональ A1B принадлежит плоскости BCD1, в этом случае легче будет рассмотреть квадрат AA1B1B, так как по свойству квадрата его диагонали точкой пересечения деляться на 2, и пересекаются под прямым углом, то половина диагонали AB1 будет расстоянием от точки до плоскости. Если где-то неправ сообщите об этом в комментарии.
Похожие вопросы
Предмет: Русский язык,
автор: lenkapeka
Предмет: Английский язык,
автор: Lampochkina
Предмет: Русский язык,
автор: valievaleysan
Предмет: Математика,
автор: N30032004
Предмет: Алгебра,
автор: Патриот48