Предмет: Математика,
автор: samandararis115
Решите уравнение:
(sinx-3cosx)(1+cosx)=
Нужно решение с разными способами, кидайте кто как решил
Спасибо
Приложения:
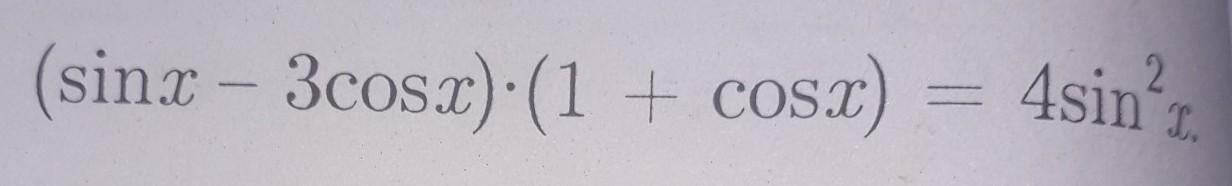
Ответы
Автор ответа:
1
.........................
Приложения:

samandararis115:
спасибо большое
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Один способ вам уже предложили.
Я предложу другой:
Выполним замену , а
, где
.
При верно:
Т.к. , то уравнению выше равносильно:
Уравнение не имеет корней.
Тогда осталось проверить, будет ли являться корнем уравнения. Получим, что да, будет. Поэтому ответ
.
Уравнение решено!
спасибо большое
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: goпрост
Предмет: Русский язык,
автор: рысгуль
Предмет: Музыка,
автор: Ника427
Предмет: Музыка,
автор: Navi557