Помогите решить пожалуйста.
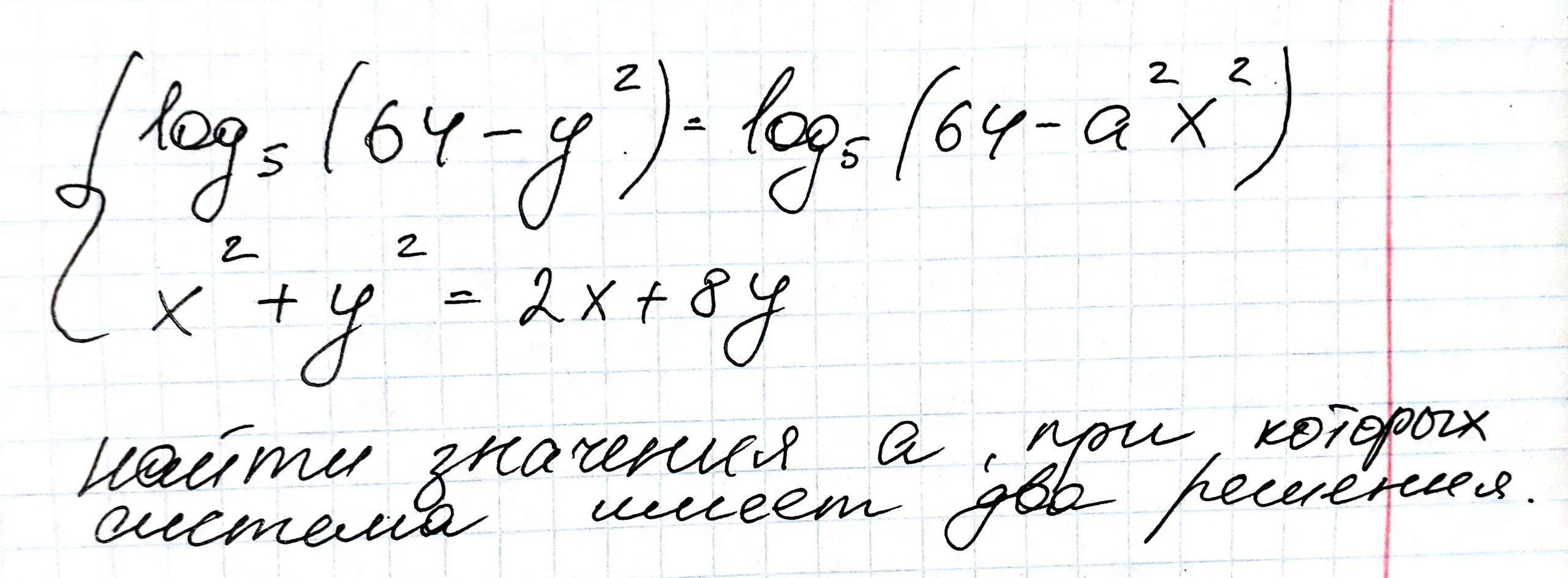
Ответы
ОДЗ:
Применяем свойство монотонности логарифмической функции:
каждое свое значение функция принимает в одной точке, поэтому если значения функции равны, то и аргументы равны.
Система принимает вид:
Если x >0; y>0 или x <0; y <0 или если x<0; y >0 или x <0; y >0
или
Решаем каждую систему способом подстановки:
или
или
или
или
или
При x >0; y>0 или x <0; y <0 или при x<0; y >0 или x <0; y >0
т. е
xy >0 или xy <0
⇒ a >0 или
⇒ a >0
Видно, что обе системы имеют общее решение х=0; y=0
Значит, чтобы выполнялось требование задачи
второе решение одной из систем не должно удовлетворять ОДЗ.
или
или
или
или
Получаем 4 неравенства:
⇒
нет таких а; D <0
или
⇒
⇒
или
⇒
нет таких а; D <0
или
⇒
⇒
При a ∈(-∞;-4] U [4; +∞) одно из решений системы не входит в ОДЗ, значит система имеет ровно 2 решения
C учетом условия: a > 0
О т в е т. [4; +∞)
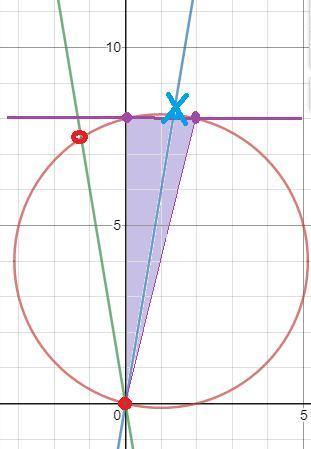
Так как второе уравнение данной системы
⇔
представляет собой уравнение окружности с центром (1;4) и R=√17, которая проходит через (0;0)
а уравнение - пара вертикальных прямых, также проходящих через начало координат и пересекающих окружность каждая в двух точках, одна из которых (0;0)
Требование задачи (c учетом ОДЗ: |y|<8) выполнено, если одна из вертикальных прямых (синяя) пересекает окружность внутри угла, образованного осью Оу и прямой, соединяющей точку (2;8) с началом координат, т. е прямая y=4x является границей указанной области: [4; +∞)