Question

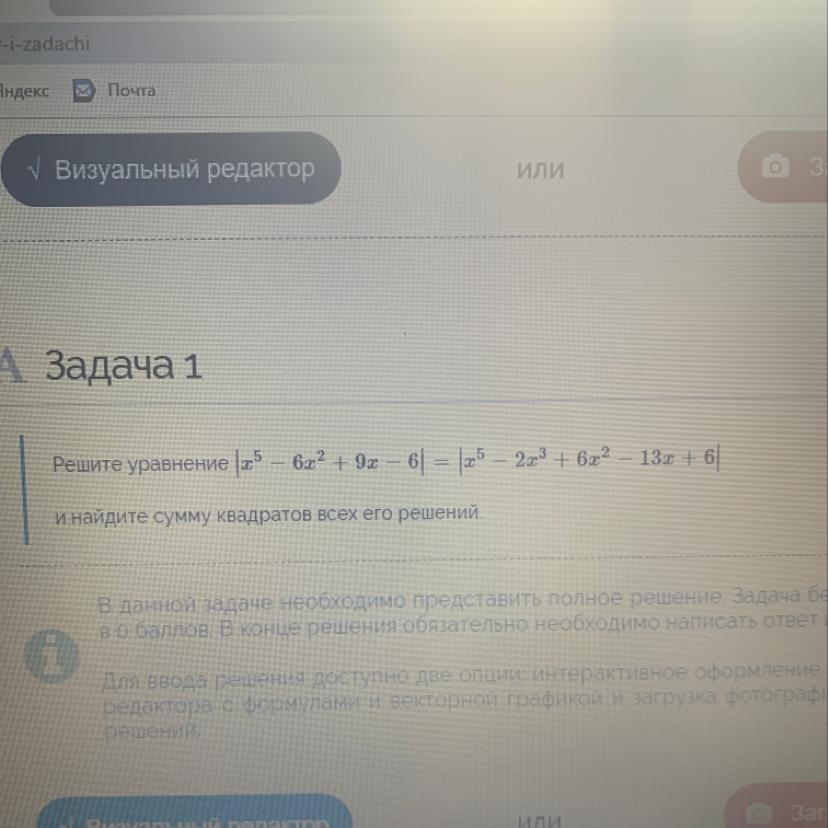
Решите пожалуйста уравнение полностью с решением и объяснением даю 15 баллов пожалуйста

Answer 1

Раскроем модули и решим 2 уравнения.

Answer 2

$|x^{5} -6x^{2} +9x-6| = |x^{5} -2x^{3} +6x^{2} -13x+6|$

По формуле |x| = √x^2 имеем :

$\sqrt{ (x^{5} -6x^{2} +9x-6)^{2}} = \sqrt{(x^{5} -2x^{3} +6x^{2} -13x+6)^{2} } \\(x^{5} -6x^{2} +9x-6)^{2}=(x^{5} -2x^{3} +6x^{2} -13x+6)^{2} \\(x^{5} -6x^{2} +9x-6)^{2}-(x^{5} -2x^{3} +6x^{2} -13x+6)^{2} = 0$

По формуле x^2-y^2 = (x-y)(x+y) имеем :

$(x^{5} -6x^{2} +9x-6-x^{5} +2x^{3} -6x^{2} +13x-6)(x^{5} -6x^{2} +9x-6+x^{5} -2x^{3} +6x^{2} -13x+6) = 0\\(2x^{3}-12x^{2} +22x-12)(2x^{5} -4x-2x^{3} )=0\\2(x^{3}-6x^{2} +11x-6)2x(x^{4} -2-x^{2} )=0\\4x(x-1)(x-2)(x-3)(x^{2} +1)(x^{2} -2) = 0\\x=0\\x = 1\\x=2\\x=3\\x=\sqrt{2} \\x = -\sqrt{2}$

$0^{2} +1^{2} +2^{2} +3^{2} +\sqrt{2} ^{2} +(-\sqrt{2})^{2} =0+1+4+9+2+2 = 18$

Ответ :

1) корни : 0, 1, 2, 3, √2, -√2

2) сума квадратов корней : 18