Предмет: Математика,
автор: Myamay
Объясните, пожалуйста, азы математики. Не могу понять как работать с 3√х. Понимаю, что такое первоообразная и как интеграл решается тоже знаю, но видимо плохо знаю подкоренные уравнения, раз не понимаю (1)откуда взялась 1/2 и (2)почему в итоге будет 2х√х. Объясните два этих момента, спасибо
Приложения:
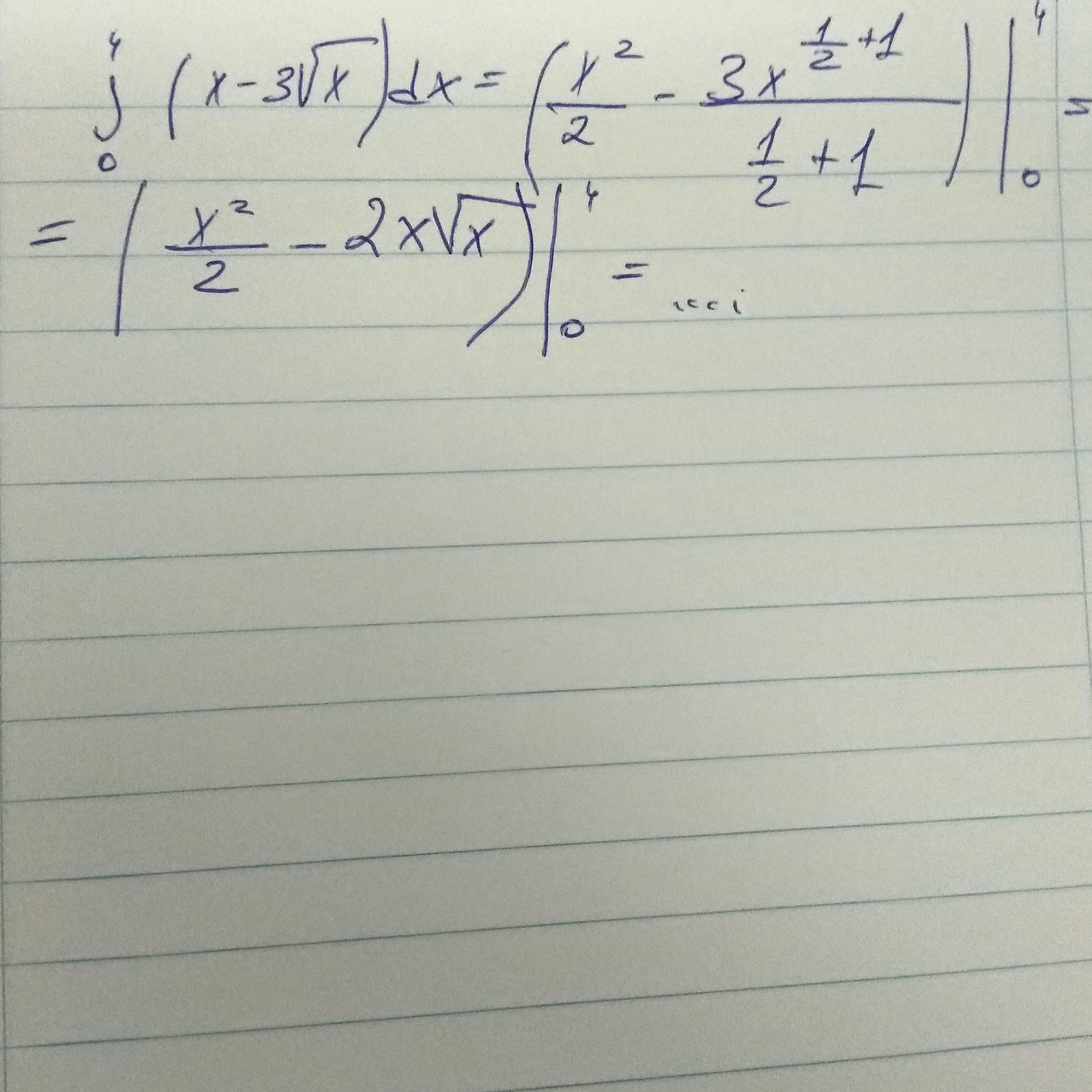
zzyto1:
ты не с корнями неумеешь работать, а со степенями
не умеешь*
ща напишу как надо
точнее, как получилось то, что получилось
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
- по определению. В выражении из условия мы вычисляем интеграл.
(с - константа) Если подставить твои значение,то получим:
я в интеграле допустил ошибку, там от a до b надо дописать
Спасибо, а то я где-то упустил про √х и всегда запарывался при решении
Похожие вопросы
Предмет: Английский язык,
автор: kisonikas
Предмет: Русский язык,
автор: sveta9904921
Предмет: Русский язык,
автор: teranobass
Предмет: Математика,
автор: Radonline
Предмет: Математика,
автор: rifat455