Question

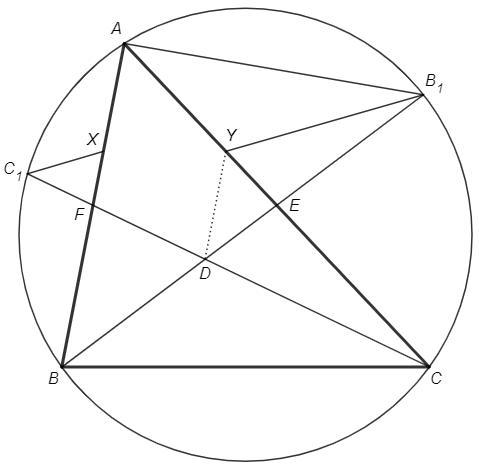
В треугольнике ABC продолжения медиан из вершин B и C пересекают описанную окружность в точках B₁ и C₁ соответственно. На стороне AB выбрана точка X, а на стороне AC − точка Y так, что BX=2AX, CY=2AY. Докажите, что ∠BXC₁ =∠CYB₁.

Answer 1

D - центроид; E, F - основания медиан

CD/DF =CY/AY =2/1 => YD||AB (теорема о пропорциональных отрезках)

∠AB₁B=∠ACB (опираются на одну дугу)

∠AEB₁=∠BEC (вертикальные)

△AEB₁~△BEC (по двум углам), AE/BE=B₁E/CE

YD||AB => AE/BE=YE/DE => YE/DE=B₁E/CE

△YEB₁~△DEC (по двум пропорциональным сторонам и углу между ними), ∠EDC =∠EYB₁=∠CYB₁

Аналогично ∠FDB=∠BXC₁

∠EDC=∠FDB (вертикальные) => ∠CYB₁=∠BXC₁