Предмет: Математика,
автор: samandararis115
При каких значениях b, уравнение
 не имеет решений
не имеет решений
Приложения:
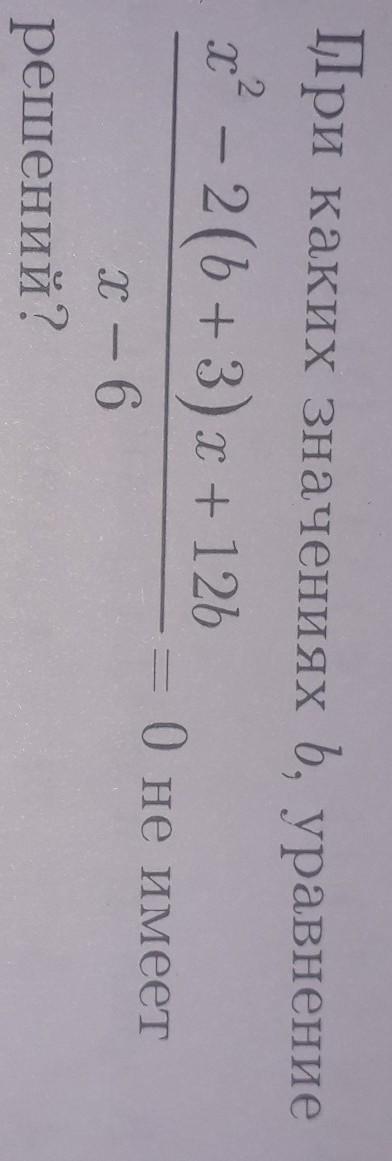
Ответы
Автор ответа:
1
Ответ:
Ответ в приложении.
Пошаговое объяснение:
1) Рассмотрим случай, когда у уравнения будет один корень. В этом случае b=3, подставляем в исходное уравнение, получаем, что корнем является 6, но это посторонний корень, значит, корней нет.
2) Рассмотрим случай, когда у уравнения нет корней, то есть дискриминант меньше нуля. Таких значений нет.
3) Рассматривать случай, когда дискриминант больше 0 не имеет смысла, потому что у нас всегда будет два или один (в том случае, когда один из корней посторонний) корней.
samandararis115:
спасибо, но в конце формула не очень понятно
Похожие вопросы
Предмет: Русский язык,
автор: ElizavetaT10
Предмет: Другие предметы,
автор: ciroga
Предмет: Русский язык,
автор: foks0605
Предмет: Биология,
автор: diana2003ru
Предмет: Математика,
автор: геллі