геометрия 8 класс помогите пожалуйста срочно

Ответы
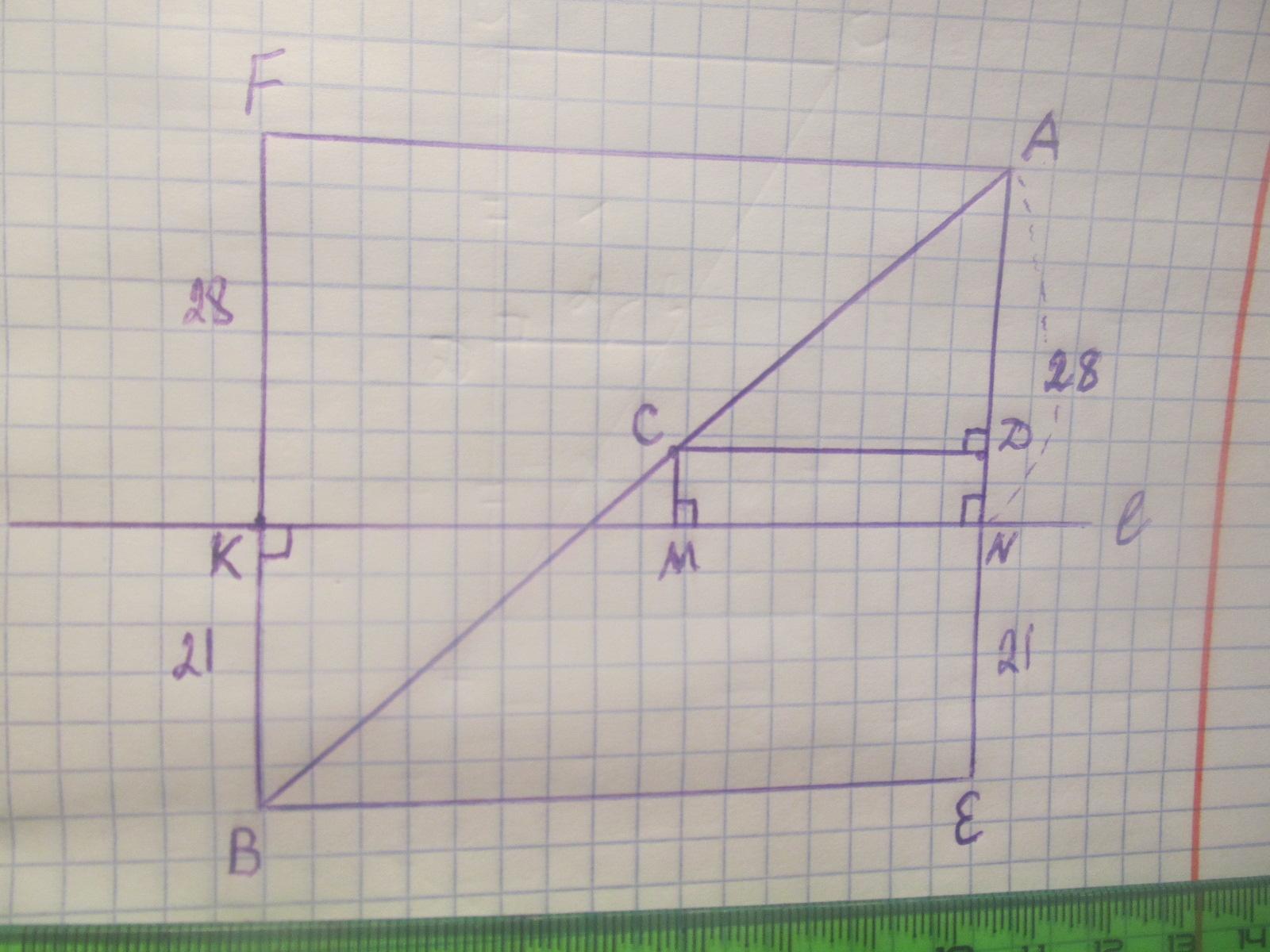
Отрезок АВ пересекает прямую L, причем точка А удалена от прямой L на 28 см, а точка В - на 21 см. Точка С - середина АВ. (рис.) На каком расстоянии от прямой L находится точка С?
———
Ответ: 3,5 см
Объяснение:
Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно от данной точки до этой прямой.
КВ⊥L=21 см, АМ⊥L=28 см. Отрезки КВ и АМ параллельны по свойству перпендикуляров, проведенных на плоскости к одной прямой. Соединив А и К, В и М, получим трапецию АКВМ, в которой АВ и КМ - диагонали, а средняя линия РТ проходит через т.С (см. рисунок).
РТ=(КВ+АМ):2=24,5 см
РС и ОТ - средние линии ∆ АКВ и КМВ соответственно и равны КВ:2=10,5 см каждая.
Расстояние от т.С до прямой L равно РТ-2•10,5=24,5-21=3,5 см.

Дано: прямая L; отрезок АВ; AN⊥L; BK⊥L; CM⊥L; AN=28 см; ВК=21 см; АС=ВС; СМ - ?
-----------------------------------------------------------------------------------------
Если точка удалена от прямой, то ее расстояние до прямой измеряется длиной перпендикуляра, опущенного из точки на прямую. Опустим перпендикуляры из т.А; т.В и т.С на прямую L.
Достроим фигуру до прямоугольника BFАE. Т.С - середина его диагонали. Проведем СД⊥АЕ или ║ L.
СMNД - прямоугольник. Т.Д - середина АЕ, т.к.
Δ АСД и Δ АВЕ - прямоугольные и подобные по острому углу А. По условию С - середина АВ ⇒ т.Д - середина АЕ.
АД=(AN+NE) : 2=(28+21) : 2=49 : 2=24,5 см.
ДN=AN-AД=28-24,5=3,5 см.
СМ=ДN=3,5 см.
Ответ: т.С находится на расстоянии 3,5 см от прямой L.