Предмет: Математика,
автор: topandelfromhill
Помогите с решением)
Приложения:
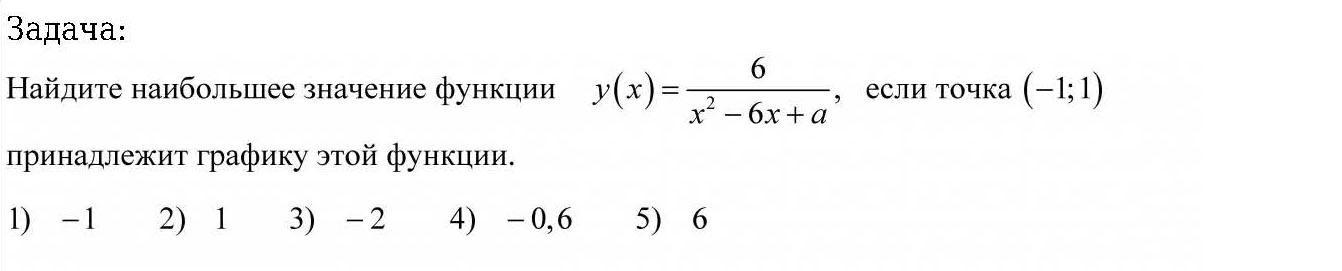
Ответы
Автор ответа:
0
Ответ:
-0.6
Пошаговое объяснение:
Точка (-1;1) принадлежит графику, значит она удовлетворяет функции. Подставляем координату этой точки в функцию и находим параметр a. (Смотри скрин)
Значит функция принимает вид:
Вычисляем производную:
(Если нужно подробно расписать - напиши в комменты)
Находим экстремумы функции:
x=3
На -∞ и ∞ Функция убывает
Значит максимальное значение она принимает в точке x=3
Находим значение:
============
Не забывайте нажать "Спасибо", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
Приложения:
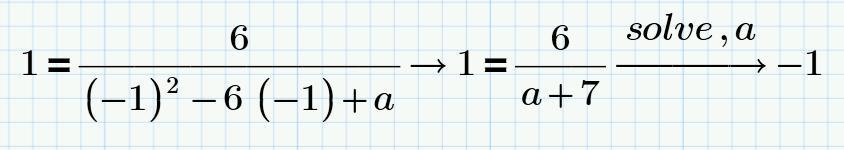
Похожие вопросы
Предмет: Русский язык,
автор: Kate3608
Предмет: Русский язык,
автор: shaydurova1988
Предмет: Русский язык,
автор: димулька2001
Предмет: Химия,
автор: эльказоид
Предмет: Математика,
автор: Панда1789хц