Предмет: Математика,
автор: vladimirsemeryuk
Упростите данное выражение:
Приложения:
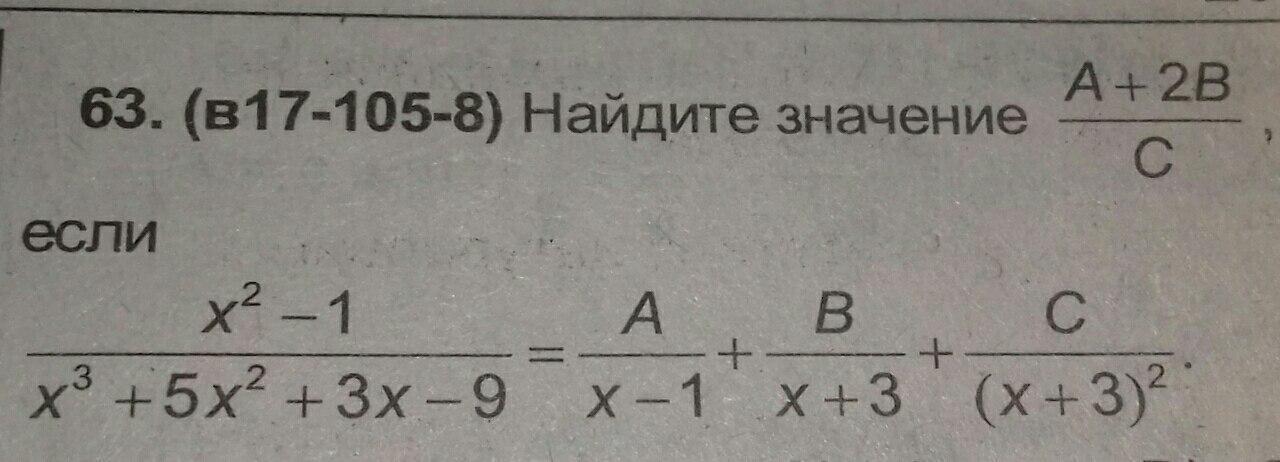
Ответы
Автор ответа:
1
Ответ:
-1
Пошаговое объяснение:
Приведём правую часть к общему знаменателю:
Знаменатель первой дроби раскладывается на множители:
Коэффициенты перед x², x и свободный член соответственно равны:
Действительно,
DNHelper:
На самом деле можно было просто раскрыть скобки в знаменателе второй дроби и убедиться в том, что знаменатели равны, но я всё же объясню, как можно на множители разложить: приравняем выражение к нулю. Сразу в глаза бросается корень x = 1. Значит, можно разложить выражение на (x-1)(что-то). Чтобы найти это что-то, нужно поделить столбиком исходное выражение на x-1. Тогда получим (x-1)(x^2+6x+9)=(x-1)(x+3)^2
Похожие вопросы
Предмет: Английский язык,
автор: alicham96
Предмет: Русский язык,
автор: Pomodoro
Предмет: Русский язык,
автор: 00тропинка00
Предмет: Химия,
автор: linas1981
Предмет: История,
автор: Darkness007