Предмет: Математика,
автор: vladimirsemeryuk
Упростите данное выражение:
Приложения:
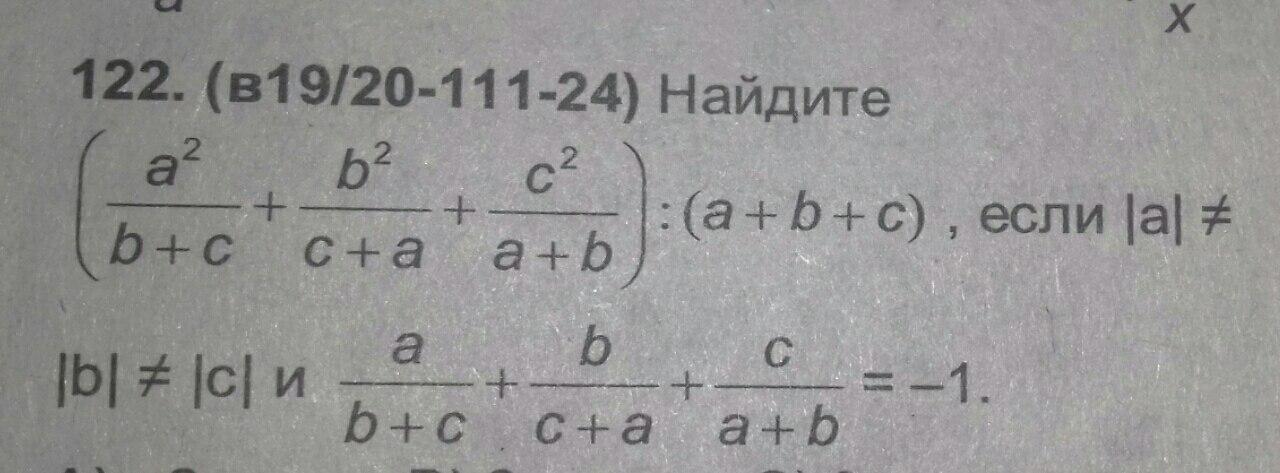
Ответы
Автор ответа:
1
Ответ:
-2
Пошаговое объяснение:
Преобразуем выражение в первой скобке:
Тогда искомое выражение равно:
Приведём дроби левой части известного выражения к общему знаменателю:
Чтобы получить из этой дроби искомое выражение, нужно вычесть дробь
Значит, искомое выражение равно
Похожие вопросы
Предмет: Английский язык,
автор: 14122002abram
Предмет: Другие предметы,
автор: tamilavasilenc1
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: kosmoskom