Предмет: Математика,
автор: sproff
Как были выполнены преобразования
Приложения:
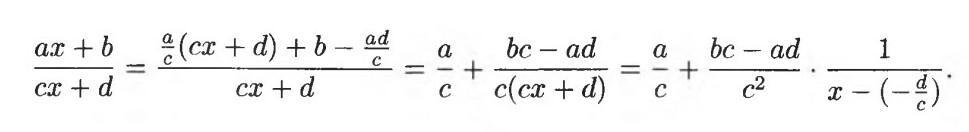
Ответы
Автор ответа:
0
В первом преобразовании нужно получить cx+d из ax+b. Пусть у нас есть cx+d. Но у нас было ax+b, поэтому нужно вернуться к этому выражению. Перед x должно стоять a. Тогда поделим cx+d на c и умножим на a: . Чтобы было ax+b, нужно прибавить b и отнять ad/c:
. Таким образом,
Во втором преобразовании числитель почленно разделили на cx+d:
В третьем преобразовании в знаменателе второй дроби вынесли c за скобку и всё, что без x, записали отдельной дробью:
Похожие вопросы
Предмет: Английский язык,
автор: sadykova12
Предмет: Русский язык,
автор: jliaparaskevova
Предмет: Другие предметы,
автор: dzuba86
Предмет: Химия,
автор: kombarov291