Предмет: Алгебра,
автор: MoonLight8224
Алгебра 11 класс. 2 примера 20 баллов
Приложения:
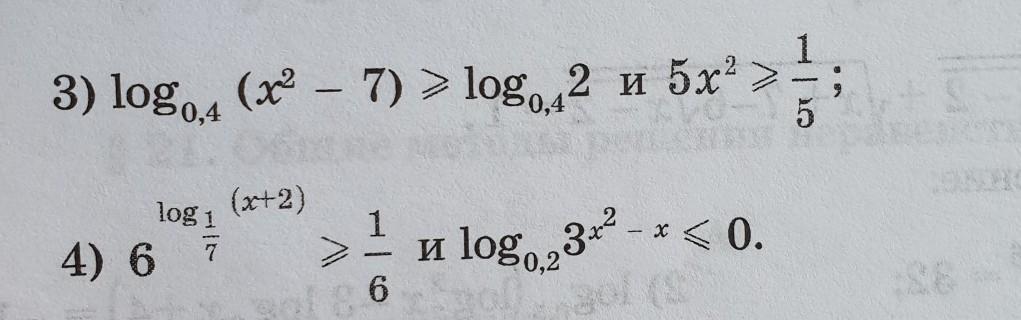
NNNLLL54:
это системы ? и где 20 баллов ?
нечайно не сделала 20 баллов
да это системы
Ответы
Автор ответа:
0
Ответ:
перезагрузи страницу, редактор формул отобразит текст...
Похожие вопросы
Предмет: Английский язык,
автор: Repukylana
Предмет: Русский язык,
автор: Pacolebo
Предмет: Русский язык,
автор: GuFFI2112
Предмет: История,
автор: Darkness007