Предмет: Геометрия,
автор: annrnb
Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по разные стороны от прямой KL. Докажите, что прямые PQ и KL перпендикулярны.
Ответы
Автор ответа:
1
Ответ:
НИЖЕ
Объяснение:
На отрезке KL возьмем т.О так что КО=ОL
Радиусы окружности ,с центром Р, равны ⇒ ΔРОК-равнобедренный , медиана РО является высотой.
Радиусы окружности ,с центром Q, равны ⇒ ΔQОК-равнобедренный , медиана QO является высотой.
Из точки О исходит два перпендикуляра к КL⇒ РQ⊥КL
Приложения:
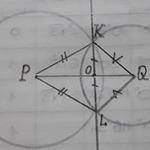
marshal500:
нужен чертеж
Похожие вопросы
Предмет: Русский язык,
автор: mrkatynenko
Предмет: Русский язык,
автор: мака1987
Предмет: Русский язык,
автор: vereshchaginao2
Предмет: Математика,
автор: sevarochka2321