Предмет: Математика,
автор: danillip
Помогите прошу кто сможет
Приложения:
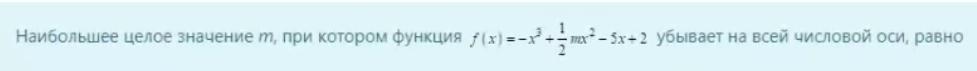
mathgenius:
Из данных m выбираем наибольшее целое
производная -квадратичная функция и с неопределенным коэффициентом
точно , 7! все верно
Дискриминант производной неположителен
То есть 7 - верный ответ
Верно?
да, дискриминант здесь не нужен
вообще можно было через вершину паработы-графика производной
ув все равно зависит от дискриминанта
решение эквивалентное
Ответы
Автор ответа:
1
Ответ :7
Пошаговое объяснение:
Чтобы функция убывала на всей числовой оси, необходимо чтобы скорость роста функции (производная) была не положительной.
f'(x) = -3x^2 + mx -5 <=0 при любом x
3x^2 -mx+5 >=0, при любом x
Поскольку у данной параболы : a=3>0, то это случится, когда D<=0
m^2 -60 <=0
m^2<=60
Откуда наибольшее целое m = 7 ( 7^2= 49 <64 ; 8^2=64 >60 )
Автор ответа:
1
Ответ:
7
Пошаговое объяснение:
Найдем производную:
Функция будет убывать, если ее производная отрицательна
Левая часть неравенства задает параболу, ветви которой направлены вниз, значит, чтобы неравенство выполнялось для всех x, нужно, чтобы ее дискриминант был отрицателен
Наибольшее целое, меньшее √60 - это 7
В случае многочлена знак должен быть строгим, это бесспорно, но существуют такие функции, где могут быть промежутки постоянства конечной длинны
Про спор в данном примере , я подразумевал, что можно привести в пример массу различных функций, в которых производная может быть равна нулю , но которые абсолютно законно считаются убывающими на всей числовой прямой
Тут вопрос формальности.
Я бы тут поставил все таки знак строгого неравенства.
ну так поставьте, у вас то стоит нестрогий знак
Я имею в виду в вашем решении, что бы вы изменили.
*Вернее конечно нестрогого.
<=
я про то, что вы путаете понятия строгий и не строгий
Это была просто оговорка.
Похожие вопросы
Предмет: Русский язык,
автор: kirmuratov1
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 855t5zcy7gn
Предмет: Геометрия,
автор: 00km
Предмет: Математика,
автор: AyaHeyli