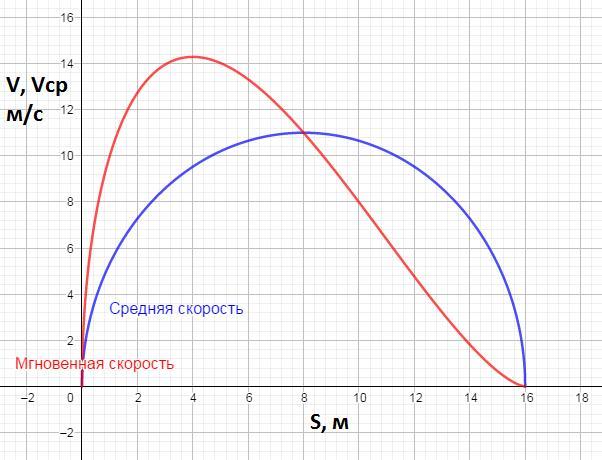
Найдите значения мгновенной скорости при S = 4 м, S = 8 м (см. рис). Ответы дайте в м/с
Ответы
Ответ:
14,3 и 11 м/с
Объяснение:
Попробуем решить эту задачу аналитически (возможно есть более изящный метод, но я его пока не вижу). Из кинематики известно следующее соотношение
(1)
На графике изображена верхняя половина эллипса с полуосями 8 и 11 единиц (насчет 11 не уверен - взял примерно). Его явное уравнение будет иметь форму
С учетом (1) инверсная зависимость времени от пути
(2)
Постараемся найти прямую зависимость S(t)
- нам повезло что уравнение разрешимо.
Мгновенную скорость легко найти, как первую производную пути по времени
(3)
Для S=4 и S=8 можно найти моменты времени по формуле (2)
с
с
Мгновенная скорость для S=4 (здесь мгновенная скорость максимальна)
м/с
Для S=8 найдем
м/с
В качестве бонуса привожу график зависимости мгновенной скорости от пути.