Предмет: Алгебра,
автор: lkadmnd
Решить систему уравнений, 10ый класс
Приложения:
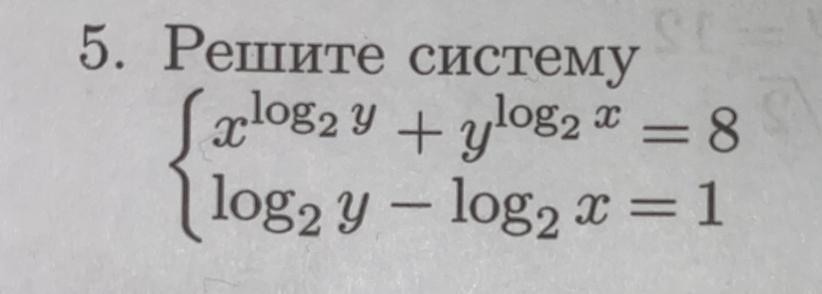
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ:
по теореме Виета:
или
или
Ответ:
lkadmnd:
спасибо большое)
Похожие вопросы
Предмет: Українська мова,
автор: svetikua2010
Предмет: Русский язык,
автор: maksim1995ivan
Предмет: Русский язык,
автор: lilililika
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: adcde