Предмет: Алгебра,
автор: LuckyST
найдите значение a+a1 если
Приложения:
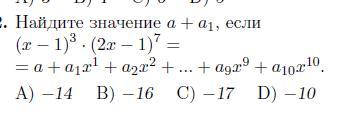
Ответы
Автор ответа:
3
Ответ:
-16
Объяснение:
a равно значению функции в левой части при x=0.
f(0)=-1*(-1)=1
a1 равно значению первой производной функции в левой части при x=0.
f'(0)=3*(-1)^2*(-1)^7+14*(-1)^3*(-1)^6=-3-14=-17
Тогда a+a1=1-17=-16
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: Nyasharu
Предмет: Українська література,
автор: KiraDidkovska9
Предмет: Қазақ тiлi,
автор: madinkaspatp
Предмет: Биология,
автор: TheLT
Предмет: Математика,
автор: саша12327