Предмет: Алгебра,
автор: thbst
Упростить и найти значение,если х=1 у=0.1 z=0.01
Приложения:
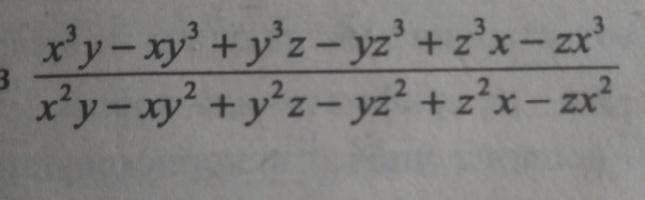
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
При x=1; y=0,1; z=0,01
получаем ответ:
1+0,1+0,01=1,11
Похожие вопросы
Предмет: Русский язык,
автор: kurbanovaelena
Предмет: Другие предметы,
автор: araichik82
Предмет: Другие предметы,
автор: Н17052000
Предмет: Биология,
автор: Aniasobaka
Предмет: Физика,
автор: ДжудиХопс34