18,13) Решите неравенство: [ arccos(-3/pi)×log(3/pi)(pi/4) ]/ [1- 2log(log2(x))(2) ] >= 0
Заранее большое спасибо!
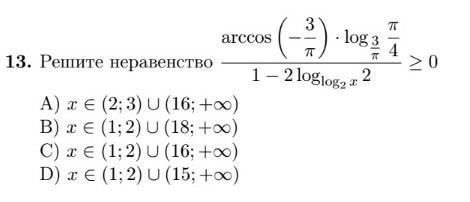
Ответы
Решение:
_______________________________________
- Рассмотрим сначала числитель неравенства и определим, какой он принимает знак (это можно сделать по причине того, что в числителе отсутствуют неизвестные).
Вспомним, что множество значений функции арккосинуса - это (а область определения
). Так как
, то такой арккосинус имеет место быть. И его значение положительно.
- Из этого, следует, что мы можем обе части поделить на
без смены знака и проблемы "деление на ноль".
Теперь посмотрим на логарифм. Его основание и подлогарифмическое выражение ( и
) соответствуют всем требованиям по ОДЗ. Также, из-за того, что и основание, и подлогарифмическое выражение находятся на промежутке
, само значение логарифма больше ноля.
- Откуда мы делим обе части на
, с равносильным переходом.
_______________________________________
Уравнение принимает вид (после сокращения на логарифм и арккосинус):
И тут можно вспомнить про ограничения (вообще, можно было их прямо сейчас не писать, и, тем более, не решать, но за пределам скобок было написано "можно"):
_______________________________________
Теперь заметим, чтобы неравенство выполнялось, необходимо, чтобы:
- При этом, в третьей строчке был применен метод рационализации: если
, то
).
Дальше - метод интервалов. Первая скобка обноляется при , а вторая - при
. Знаки на числовой оси тоже можно расставить (отмеченные точки - выколотые):
+ + + + + - - - - - + + + + +
______________________
___________
В пересечении с ОДЗ (актуально ) имеем вот такое решение:
Номер ответа - C)!
_______________________________________