Предмет: Алгебра,
автор: stepanovgleb2000
Тригонометрия 9 класс
Будьте добры, помогите пожалуйста
Приложения:
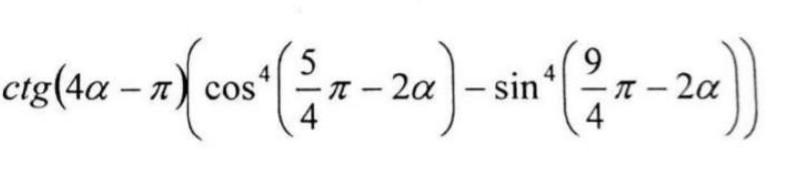
Ответы
Автор ответа:
0
Ответ:
Объяснение:
stepanovgleb2000:
эм, что?
Похожие вопросы
Предмет: Русский язык,
автор: roza83123
Предмет: Українська література,
автор: Lynxreya
Предмет: Другие предметы,
автор: veronikaqw13524zx
Предмет: Математика,
автор: Danighff