Предмет: Математика,
автор: nipice1487
Решите, пожалуйста, неравенство.
Приложения:
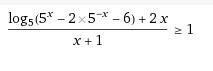
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ:
____________
Рассматриваем 2 системы:
1)
2)
1)
2)
1)
2)
1)
2)
_________
Замена для двух систем:
_________
Решаем первые части систем:
1)
2)
!!!! € вместо знака принадлежности
1) t€[-1;0) или [7;+∞)
2) t€(-∞;-1] или (0;7]
Обратная замена:
1)
система
вне системы
2)
система:
1) система:
х€ R
x не принадлежит R
вне системы:
2) x не принадлежит R
система:
х€R
1)
2)
возвращаемся в основные системы:
1)
2)
1)
2)
Ответ с учётом ОДЗ:
Похожие вопросы
Предмет: Другие предметы,
автор: matik123
Предмет: Русский язык,
автор: Doly98
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: ksushov
Предмет: Математика,
автор: denissaxno83