Question

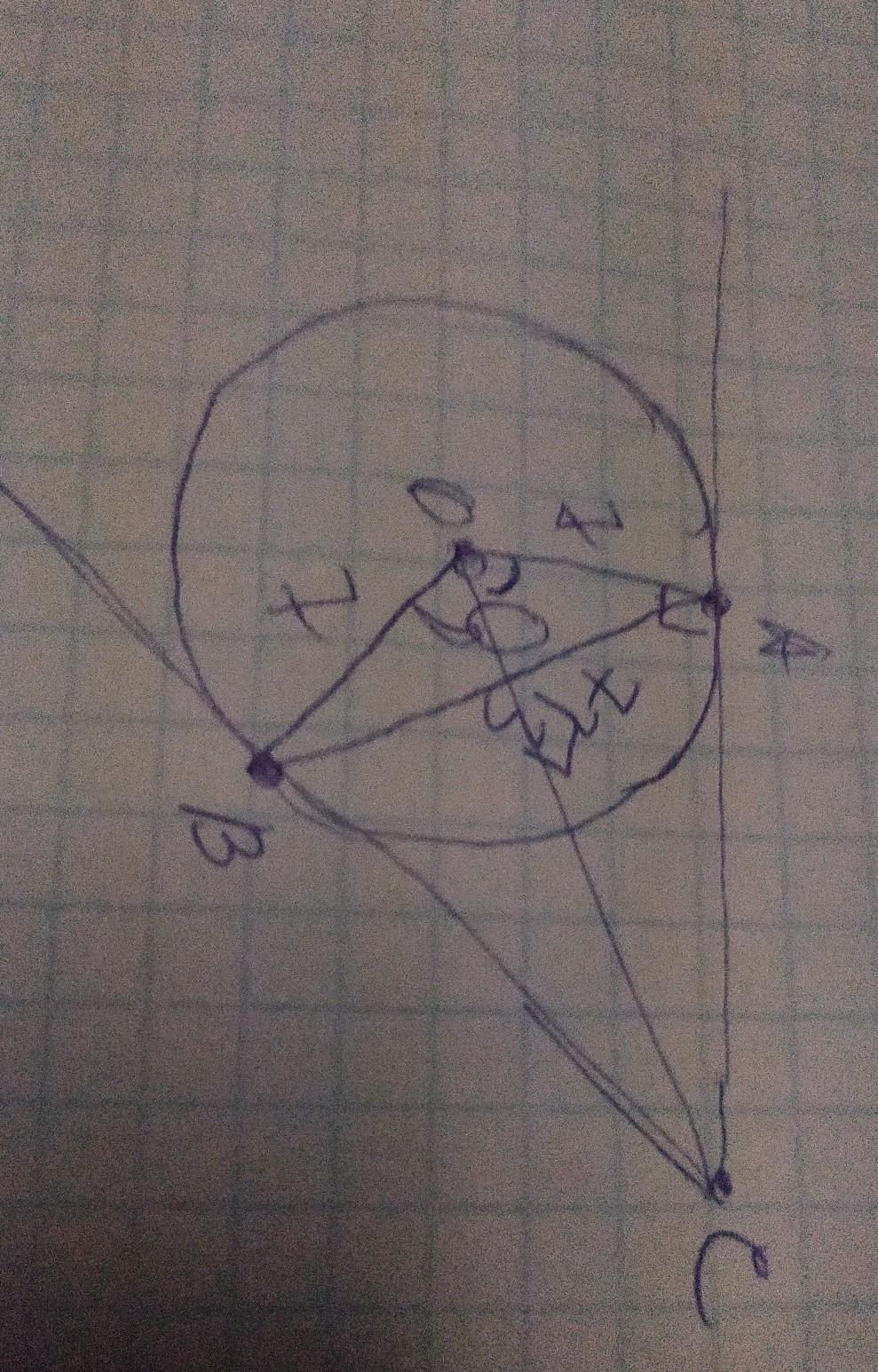
ВC и AС – отрезки касательных, проведённых к окружности с центром в точке О и радиусом 7 см так, что AВ = 7√3 см. Найдите угол АОC. Ответ дайте в градусах​

Answer 1

ВC и AС – отрезки касательных, проведённых к окружности с центром в точке О и радиусом 7 см так, что AВ = 7√3 см. Найдите угол АОC. Ответ дайте в градусах​

Объяснение:

По т. косинусов для ΔОАВ

АВ²=ОА²+ОВ²-2*ОА*ОА cos∠АОВ ,

49*3=2*49-2*49*cos∠АОВ ,

2*49*cos∠АОВ =2*49-3*49

cos∠АОВ =-1*49:(2*49) ,

cos∠АОВ =-1/2 ,  ∠АОВ=120°.

Т.к. ΔСВО=ΔСАО как прямоугольные( радиус , проведенный в точку касания перпендикулярен касательной)  по 2 катетам и общей гипотенузе, то ∠СОВ=∠СОА=120°:2=60°

Answer 2

Ответ:

60°

Объяснение:

рассмотрим полученный ∆АОВ. Он равнобедренный поскольку АО=ВО=радиусу, поэтому прямая СО делит ∆АОВ и угол АОС пополам, поэтому <АОС=<ВОС. В ∆АОВ известны 3 стороны, поэтому мы можем найти угол АОВ, используя теорему косинусов:

$\cos(aoc) = \frac{ao {}^{2} +bo { }^{2} - ab {}^{2} }{ {}^{2 \times ao \times bo} } = \frac{7 {}^{2} + 7 {}^{2} - (7 \sqrt{3} ) {}^{2} }{2 \times 7 \times 7} = \frac{49 + 49 - 49 \times 3}{98} = \frac{98 - 147} {98} = \frac{ - 49}{98} = - \frac{1}{2}$

Итак: cosAOB= –1/2=120°.

Так как угол АОС - это половина угла АОВ, то угол АОС=120÷2=60°