Предмет: Математика,
автор: Подсказочкa
При каких с уравнение x^3-x+c=0 имеет ровно одно решение?
Ответы
Автор ответа:
1
По теореме Виета произведение корней равно -c.
Очевидно, что коэффициенты не могут быть равны 0 одновременно, а значит таких с нет.
Ответ: ∅
aastap7775:
https://znanija.com/task/37808010?answeringSource=feedPersonal%2FhomePage%2F2
Далеко ходить не нужно
Если автором не уточнено иное, в подобной ситуации ни про какую комплексную область речь не идёт.
Чем Вам не нравятся комплексные числа? Автор не указал, что их не нужно учитывать.
Потому что в задачах школьного уровня про это речь не идёт.
А насколько я понимаю, решение уравнение - это такое числа x, для которого уравнение обращается в верное выражение.
А кто сказал, что это школьный уровень?
Как я писал выше, по умолчанию задача считается школьного уровня, и уровень задачи считается соответствующим установленному.
В подобных случаях*
На мой субъективный взгляд я решил задачу для x из C. Для x из R решили задачу ниже.
Автор ответа:
1
Ответ:вот
Пошаговое объяснение:
Приложения:
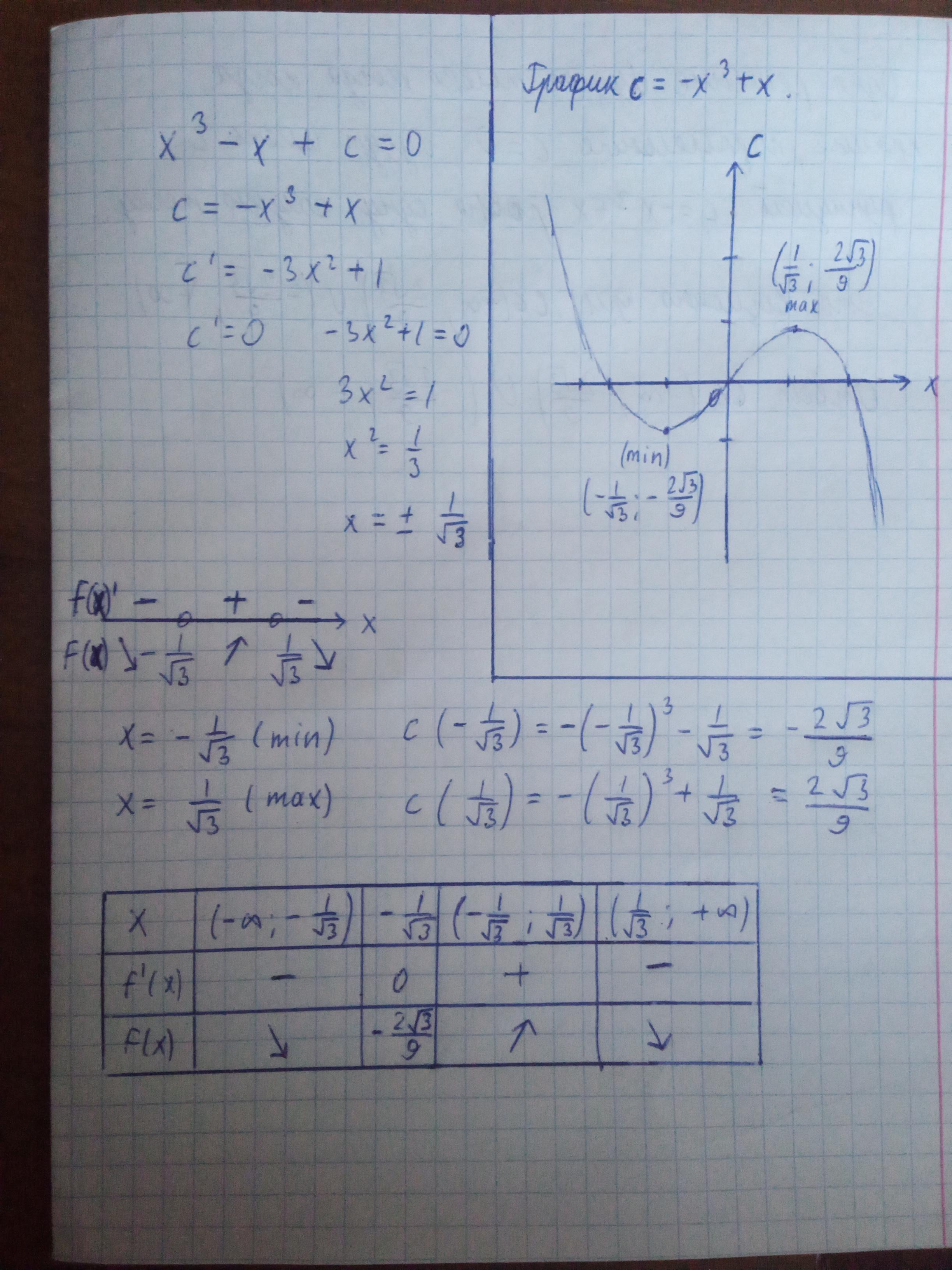

Насколько я понимаю, то с - это константа. Ее производная не может быть отличной от нуля.
Похожие вопросы
Предмет: Русский язык,
автор: almaas2
Предмет: Русский язык,
автор: Guzik23
Предмет: Английский язык,
автор: narekmariam1996
Предмет: Химия,
автор: вероника375292662124
Предмет: Алгебра,
автор: JULIA200202