В равнобокий трапеции АВСД , О-точка пересечения диагоналей. Прямая МО перпендикулярна плоскости трапеции . Доказать , что плоскости АМС и ВМД перпендикулярны

Ответы
Ответ:
Объяснение:
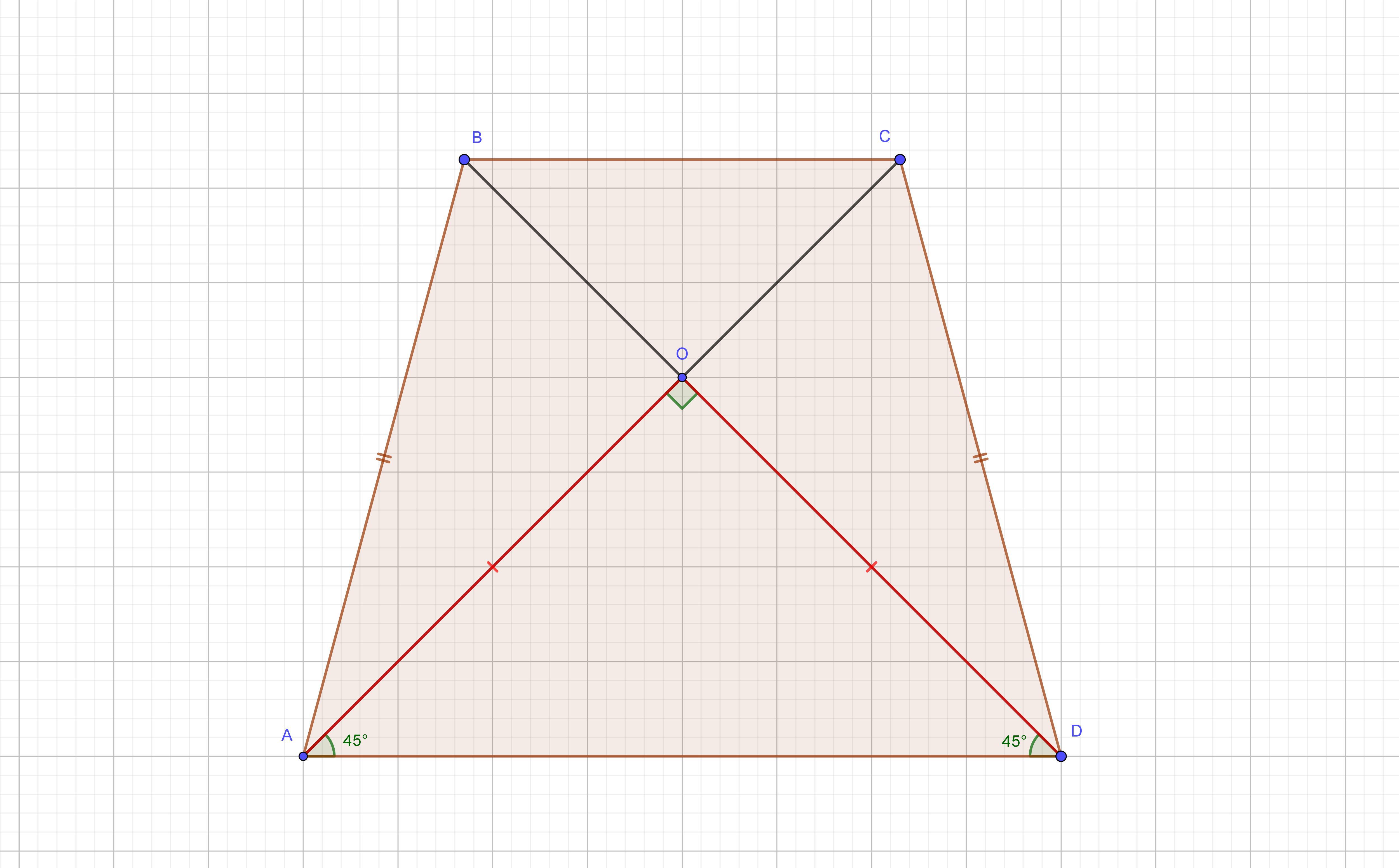
См. картинку 1.
Трапеция равнобедренная, значит диагонали равны и делятся точкой пересечения в одинаковом отношении. Следовательно AO = DO
Значит ΔAOD - равнобедренный. ⇒ ∠OAD = ∠ODA
∠AOD = 180° - 2* 45° = 90°
MO перпендикулярна плоскости трапеции, значит MO ⊥ BD и MO ⊥ AC
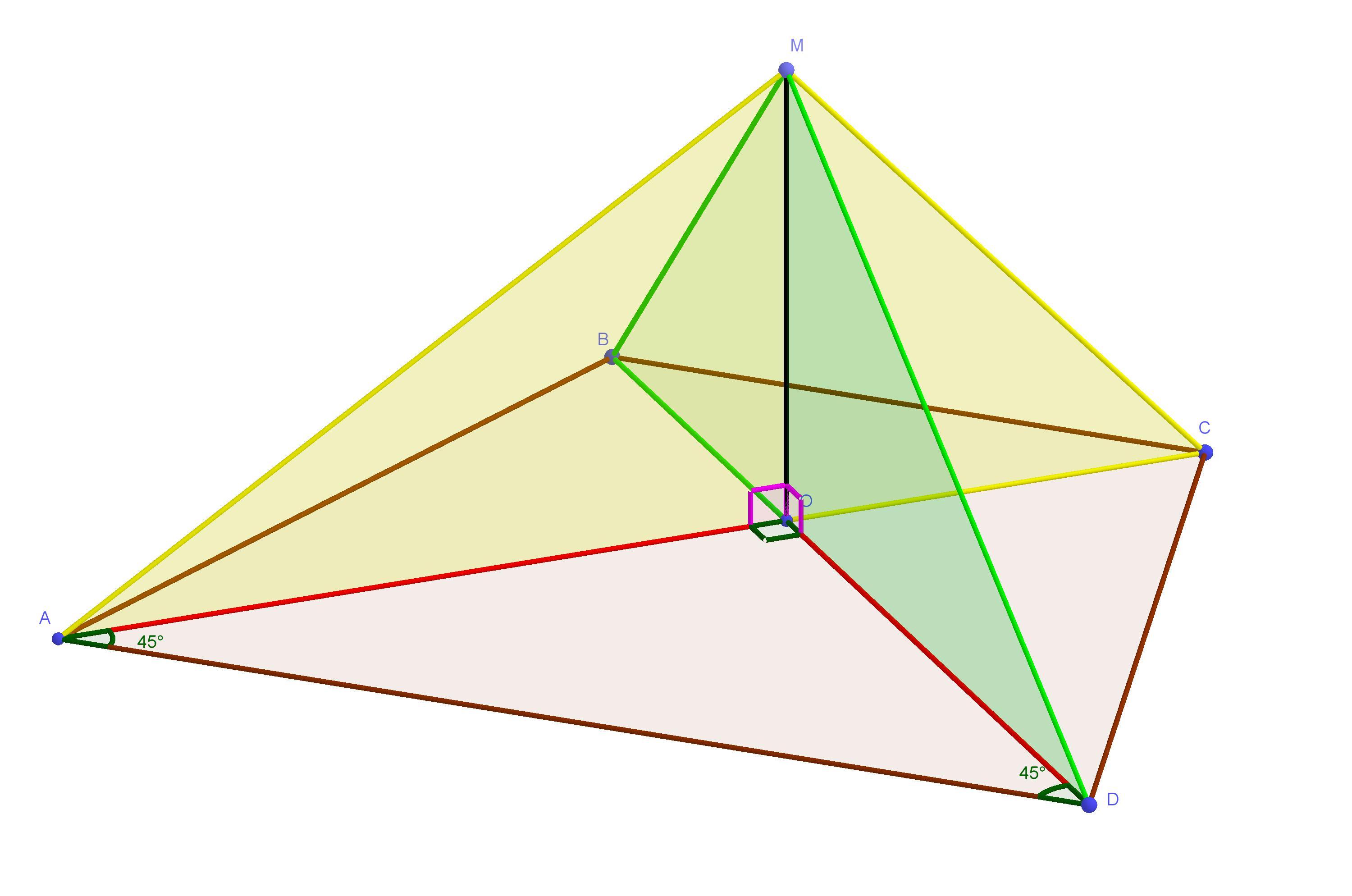
См. картинку 2.
"Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны."
(·) O ∈ BD ⇒ (·) O ⊂ BMD значит MO ⊂ BMD
AO ⊥ OM и AO ⊥ OD Следовательно AO ⊥ BMD
(·) O ∈ AC ⇒ (·) O ⊂ AMC
AO ⊥ BMD и содержится в AMC следовательно BMD ⊥ AMC ч.т.д.
============
Не забывайте нажать "Спасибо", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!