Предмет: Геометрия,
автор: pbellay
«Может поможешь мне?»
Ребро куба MNPQM1N1P1Q1 равно 2. Найдите тангенс угла между плоскостями M1QP1 и M1N1P1.
Приложения:
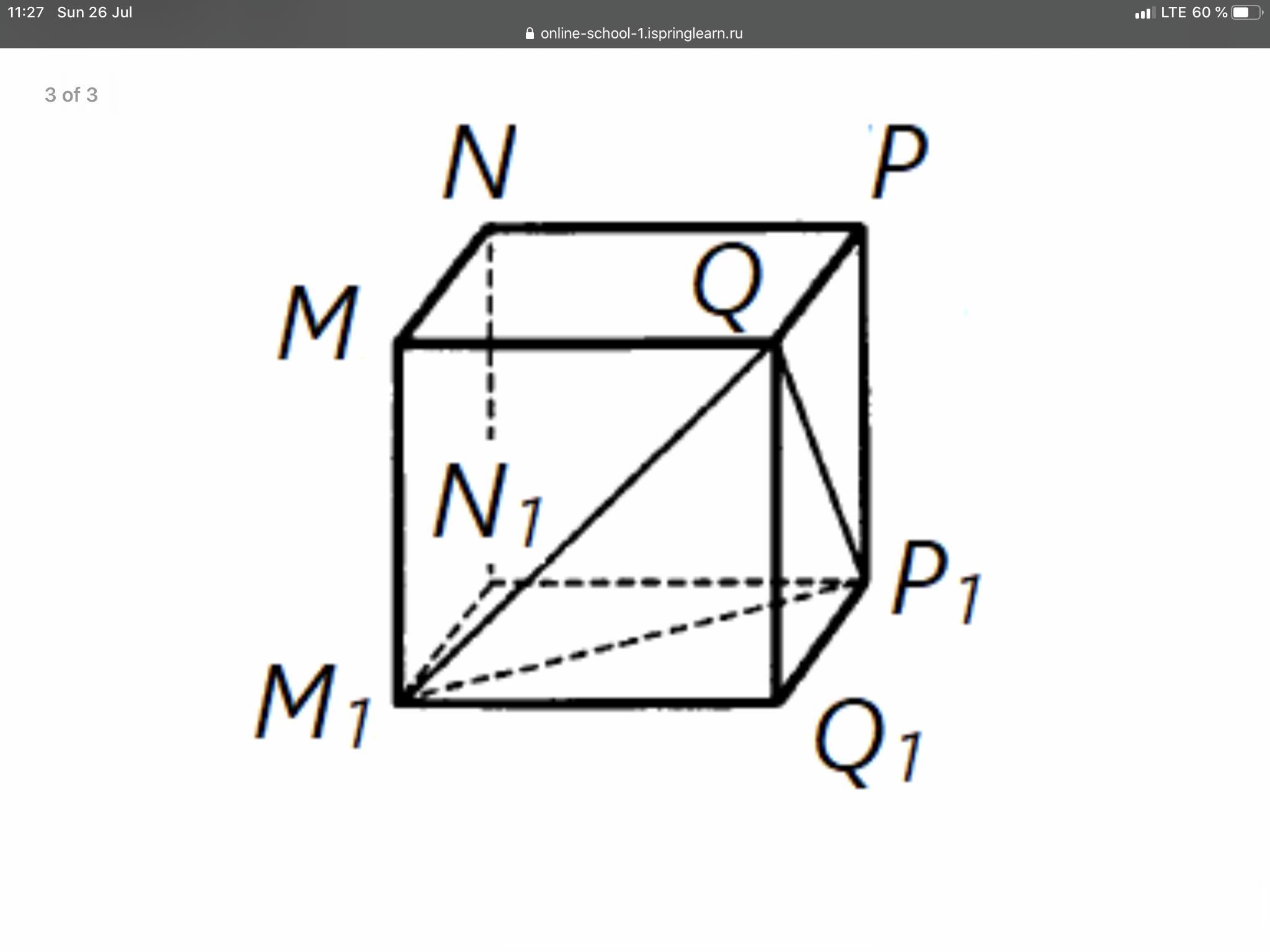
pbellay:
А это была отсылка к SC2
Ура, хоть кто-то решил помочь)
Ответы
Автор ответа:
3
Ответ:
Объяснение:
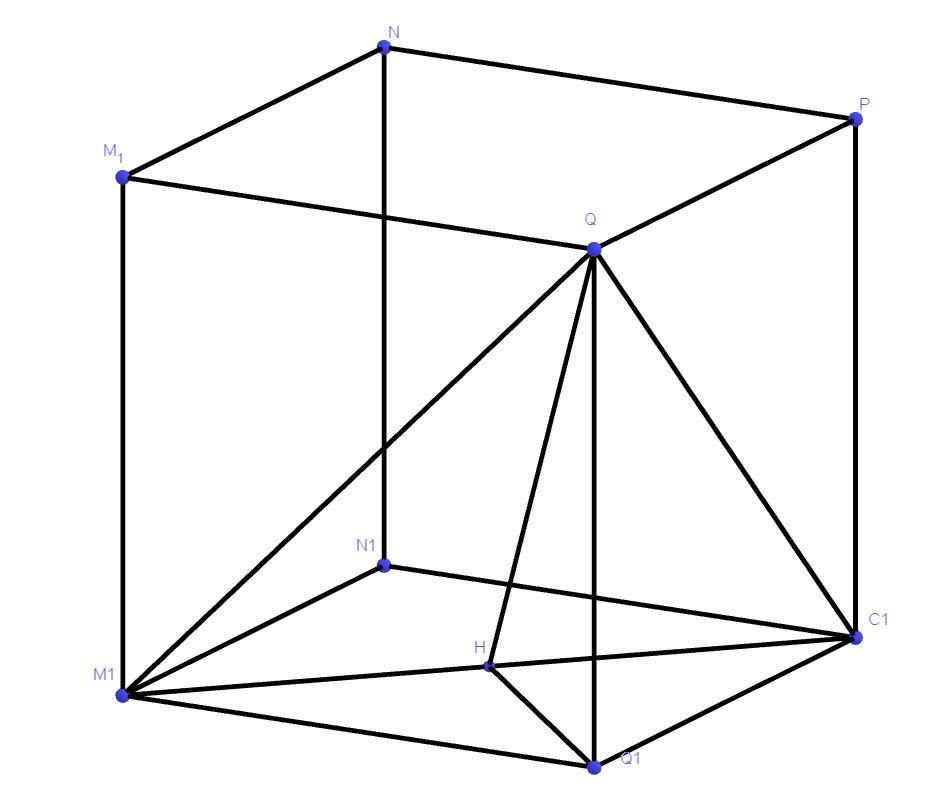
Назовем α плоскость M₁N₁P₁
Назовем β плоскость M₁QP₁
очка Q₁ также принадлежит α. (Можно доказать различными способами)
Проведем Q₁N₁
Диагонали квадрата пересекаются под прямым углом и точкой пересечения делятся пополам.
Значит Q₁H ⊥ M₁P₁
Q₁H =
QQ₁ ⊥ α т.к QQ₁ ⊥ M₁Q₁ и QQ₁ ⊥ P₁Q₁
QH ⊥ M₁P₁ по Т. о трех перпендикулярах (QQ₁ - перпендикуляр, QH-наклонная, Q₁H - проекция)
∠(α,β) = ∠Q₁HQ
tan(∠(α,β)) = tan(∠Q₁HQ) =
============
Не забывайте нажать "Спасибо", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
Приложения:
Спасибо тебе огромное - 3-из раз задаю и только ты ответил(а)
Похожие вопросы
Предмет: Русский язык,
автор: bandatzky
Предмет: Қазақ тiлi,
автор: Daniiil2002
Предмет: Русский язык,
автор: Scfrt
Предмет: Биология,
автор: Ключевская
Предмет: История,
автор: Elingva