Предмет: Математика,
автор: bazarovdamir882
Как решаются подобные уравнения?
Интересуют именно члены с модулями.
Приложения:
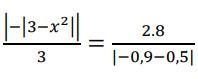

bazarovdamir882:
Не понимаю, чему равняются члены с модулем.
По определению. Если число или выражение под знаком модуля отрицательные, то противоположному числу или выражению |-3|=3. если неотрицательные, то самому этому числу или выражению |3|=3
Ответы
Автор ответа:
0
1.
|-0,9-0,5|=|-1,4|=1,4
|-|3-x²||=-(-|3-x²|=|3-x²|
⇒ 3-x²=-6 или 3-х²=6
x²=9 или х²=-3
x=±3 или нет корней
О т в е т. ±3
2.
|-1,4+0,7|=|-0,7|=0,7
|-|x²-2||=-(-|x²-2|=|x²-2|
⇒ 2-x²=-2 или 2-х²=2
x²=4 или х²=0
x=±2 или x=0
О т в е т. 0;±2
Правильно ли я понимаю, что для 6 класса - в первом уравнении ответ "нет корней", а во втором "0"?
Уравнение х²= - 3 не имеет корней. Уравнение х²=9 имеет два корня: Ответ два корня.
Автор ответа:
0
Ответ: решение на фото. Всё просто.
Пошаговое объяснение:
Приложения:
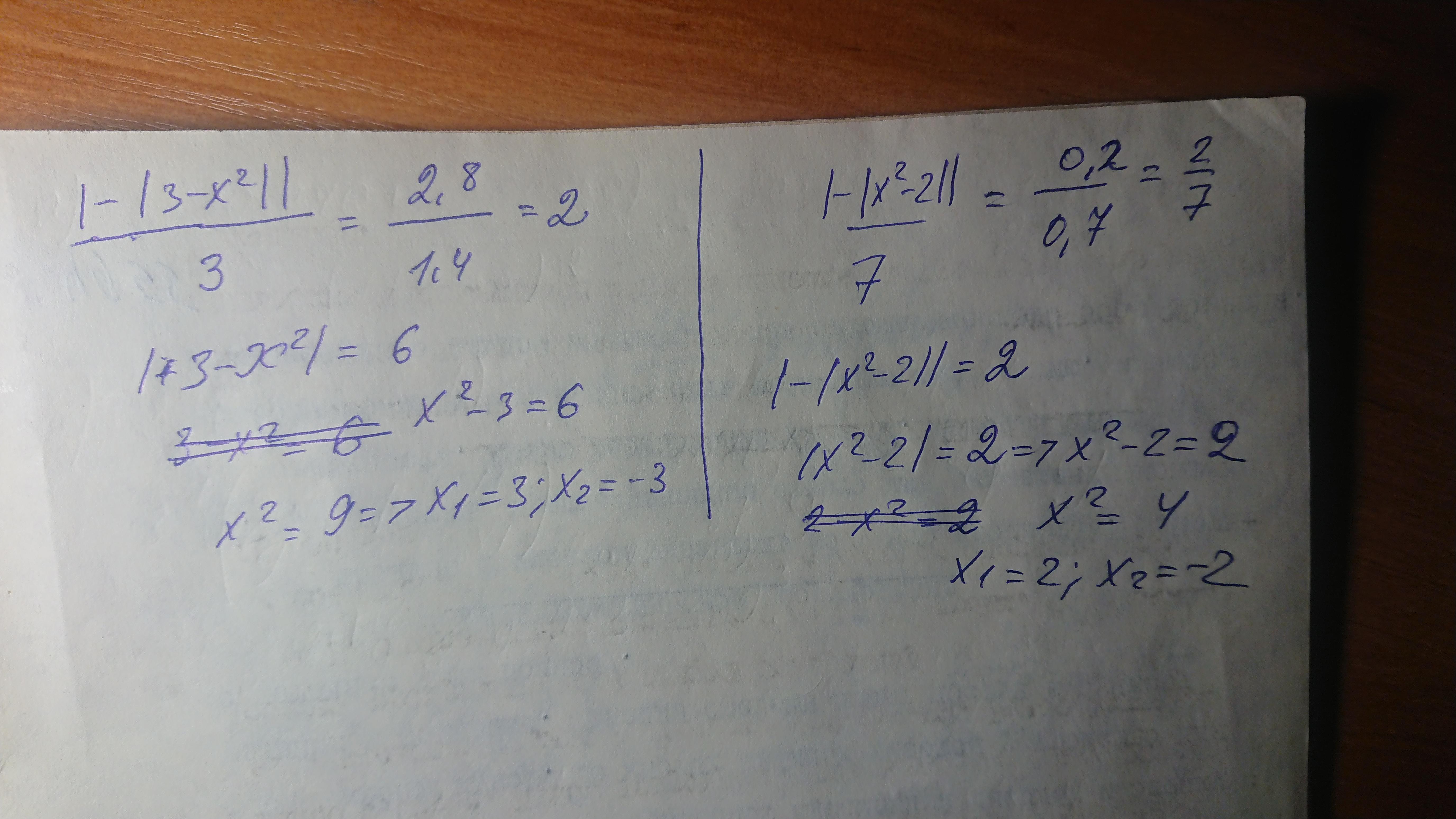
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: пахан23
Предмет: Русский язык,
автор: legi00n
Предмет: Алгебра,
автор: mishakukla
Предмет: Химия,
автор: Annase2002