Предмет: Математика,
автор: sproff
Объясните, как были сделаны преобразования
Приложения:
Ответы
Автор ответа:
1
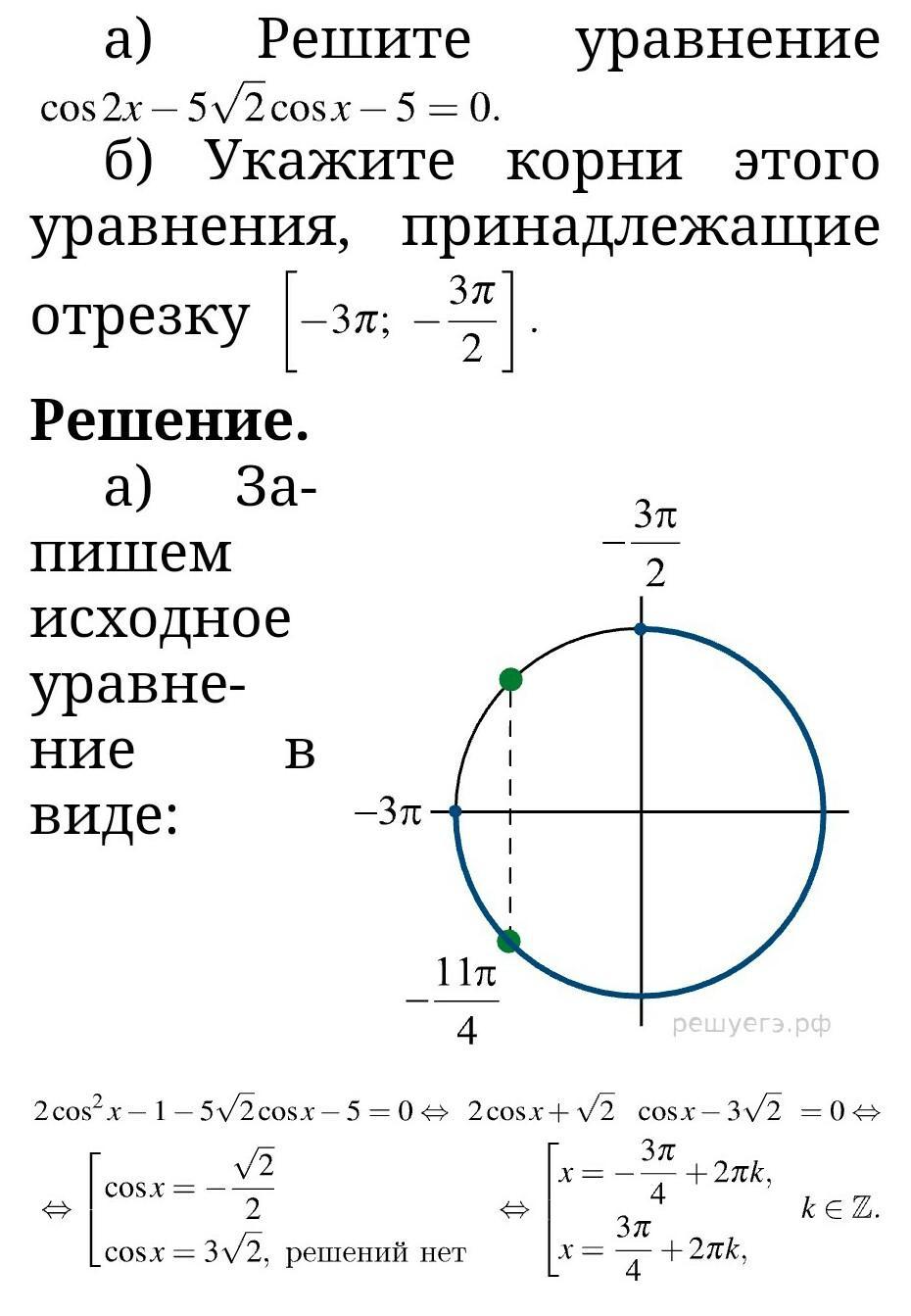
Ответ: а) x=+-3*π/4+2*π*k, где k∈Z, б) x=-11*π/4.
Пошаговое объяснение:
Так как cos(2*x)=cos²(x)-sin²(x)=2*cos²(x)-1, то данное уравнение можно записать в виде: 2*cos²(x)-5*√2*cos(x)-6=0. Полагая cos(x)=t, получаем квадратное уравнение 2*t²-5*√2*t-6=0. Оно имеет решения t1=3*√2, t2=-√2/2. Но так как /cos(x)/≤1, то значение t1>1 не годится, поэтому t=-√2/2. Решая уравнение cos(x)=-√2/2, находим x=+-arccos(-√2/2)+2*π*k=+-3*π/4+2*π*k, где k∈Z. Отсюда следует, что на интервале [-3*π;-3*π/2] это уравнение имеет единственный корень x=-11*π/4.
Автор ответа:
1
тогда
Разложим на множители :
Похожие вопросы
Предмет: Русский язык,
автор: рапрпоро
Предмет: Русский язык,
автор: veronikarony6
Предмет: Русский язык,
автор: sabisha1987
Предмет: Математика,
автор: крис9971