Question

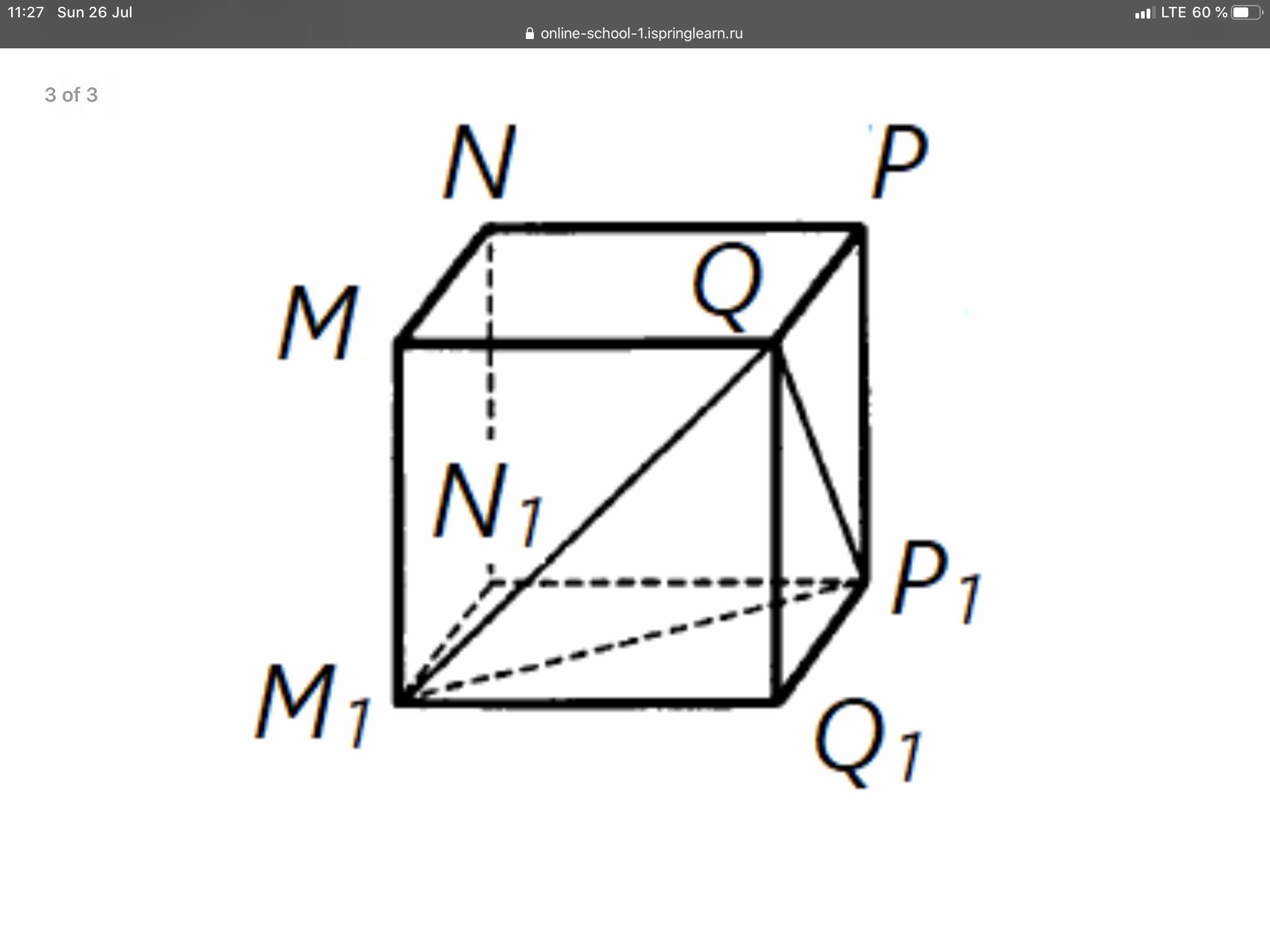
Ребро куба MNPQM1N1P1Q1 равно 2. Найдите тангенс угла между плоскостями M1QP1 и M1N1P1.

Answer 1

Ответ:

$\bold{tg}(Q_1OQ) = \dfrac{2}{\sqrt{2}}$

Объяснение:

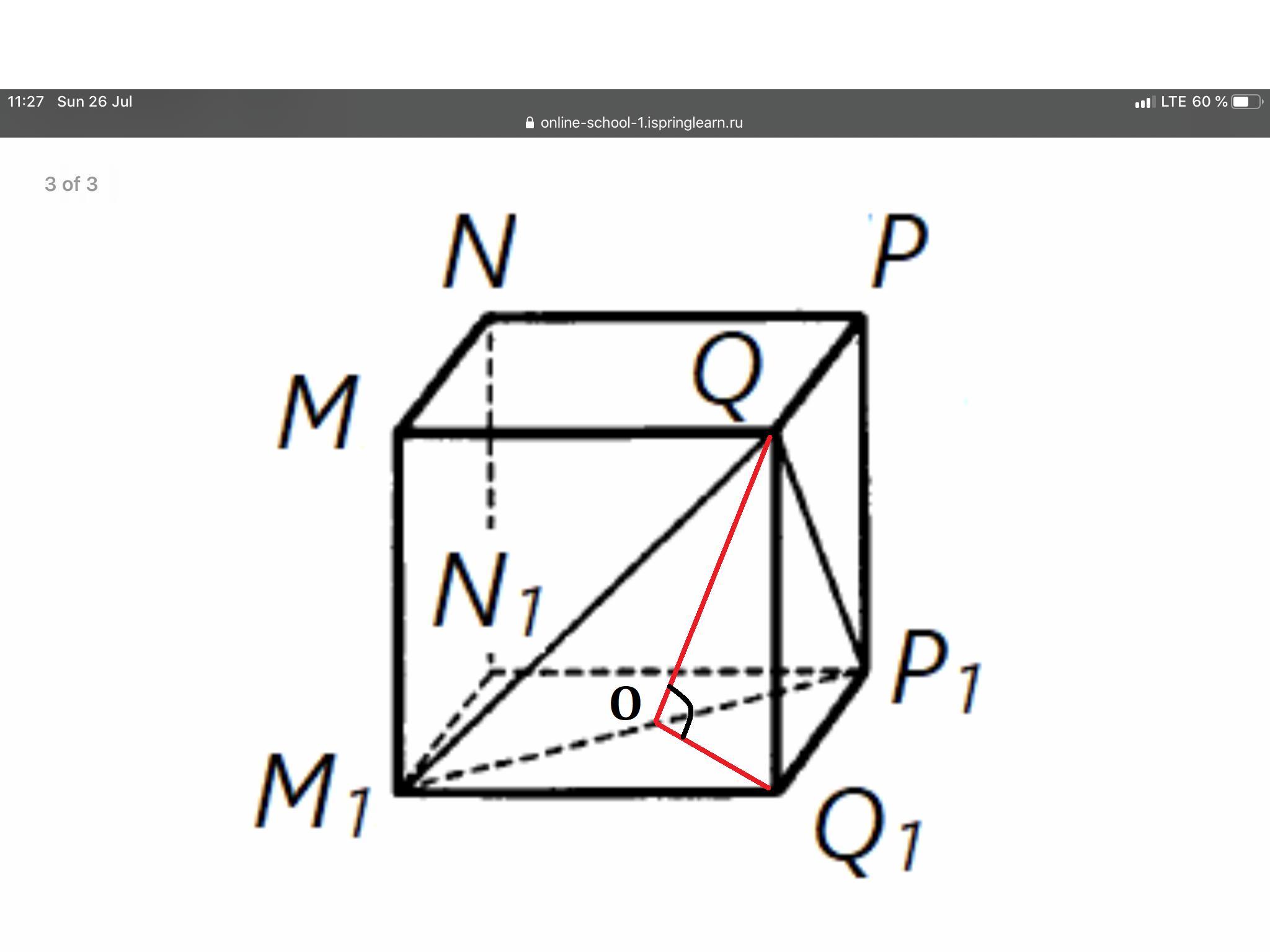
Обозначим середину диагонали $M_1P_1$ квадрата $M_1N_1P_1Q_1$ буквой $O$.

Угол между плоскостями $M_1QP_1$  и $M_1N_1P_1$ - $\angle Q_1OQ.$

$\bold{tg}(Q1OQ) = QQ_1:OQ_1$

Так как у куба все ребра равны и ребро данного куба равно $2$ ⇒ $QQ_1 = 2$

$M_1N_1P_1Q_1$ - квадрат (так как у куба все рёбра равны).

$M_1P_1 = M_1N_1 \cdot \sqrt{2} = 2\sqrt{2}$

У квадрата все диагонали равны и делятся точкой пересечения пополам.

⇒ $M_1O = OP_1 = OQ_1 = M_1P_1:2 = \dfrac{2\sqrt{2}}{2} = \sqrt{2}$

⇒ $\bold{tg}(Q_1OQ) = \dfrac{2}{\sqrt{2}}$