Предмет: Математика,
автор: Анатолий228
Помогите 14 и 15 задание
Приложения:
Ответы
Автор ответа:
1
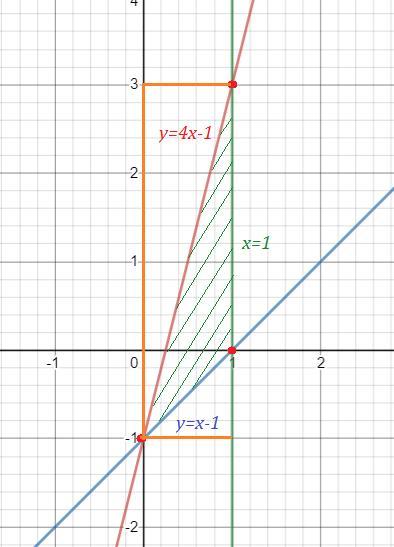
Пошаговое объяснение: см. во вложении
Приложения:

Автор ответа:
0
Ответ:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: tyutemarina
Предмет: Английский язык,
автор: QVikss
Предмет: Английский язык,
автор: BogdanovichMariya
Предмет: География,
автор: 13reasonswhy
Предмет: Алгебра,
автор: Aleksey1853