Помогите пожалуйста решить этот пример.Найти все корни уравнения на отрезке [0: 2Pi]
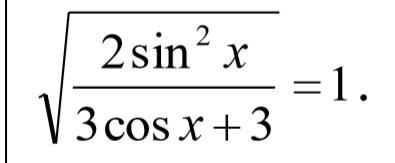
Ответы
Возводим в квадрат:
D=9-4·2=1
⇒
⇒
принадлежат отрезку [0: 2π]
Ответ: x=+-2π/3 +2πn , n∈Z
На интервале [0; 2π] : x1=2π/3 ; x2=4π/3
Объяснение:
Немного другой путь решения.
√(2sin^2(x)/(3cos(x) +3) ) = 1/√3 * √(sin^2(x)/( (1+cos(x) )/2) ) =
=1/√3 *√(sin^2(x)/cos^2(x/2) ) = |sin(x)/cos(x/2) | /√3 = =|2*sin(x/2)*cos(x/2)/cos(x/2)| /√3 = 2*|sin(x/2)|/√3
Таким образом, уравнение принимает вид :
|sin(x/2)| = √3/2
sin(x/2) =+-√3/2
1)x/2 = +-π/3 +2πN, N∈Z → x =+-2π/3 +2πr, r∈Z и r - четное
2) x/2 = π-+π/3 +2πk, k∈Z → x=+-2π/3 +2π*(2k+1) = +-2π/3 +2π*m , m∈Z и m-нечетное.
То есть эквивалентно такому решению :
x=+-2π/3 +2πn , n∈Z
На интервале [0; 2π] подходит :
x1=2π/3
x2= -2π/3 +2π = 4π/3
ОДЗ: cos(x/2)≠0 выполняется, так как при данных x |sin(x/2)≠1|