Предмет: Алгебра,
автор: egorkabystrov00
Помогите решить это пожалуйста. Лучше с максимально подробными объяснениями.
Приложения:
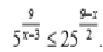
Ответы
Автор ответа:
1
Показательная функция с основанием 5 > 1 возрастает.
при x = 6
При x ≠ 6
(x-6)²≥0
значит знаменатель
⇒
О т в е т. { 6}
Похожие вопросы
Предмет: Русский язык,
автор: Mashenka20222
Предмет: Русский язык,
автор: 555333444
Предмет: Другие предметы,
автор: daniil55543
Предмет: Математика,
автор: abduvoeid