Question

в треугольнике АВС проведена высота ВD медиана ВМ и биссектриса ВК.докажите что точка К принадлежит отрезку DM.

Answer 1

Небольшая поправка. Если треугольник равнобедренный с основанием АС, то в нем все три основания высоты, биссектрисы и медианы сливаются в одну точку.

В Δ ABC точки  D, К и M - основания соответственно высоты, биссектрисы и медианы, проведенных из вершины B. Опишем около

Δ ABC окружность. Пусть Е - точка пересечения прямой BК с этой окружностью. Тогда Е будет серединой дуги AC. Поэтому прямая, проведенная через точку Е параллельно BD, перпендикулярна хорде AC и проходит через ее середину, т. е. точку M. А т.к. точки B и Е лежат по разные стороны от прямой AC, то точка К лежит между проекциями концов отрезка ЕB, т. е. между точками D и M, значит , она принадлежит отрезку DM, ч.т.д.

Answer 2

Ответ: Постарался доказать как можно более строго.

Пошаговое объяснение:

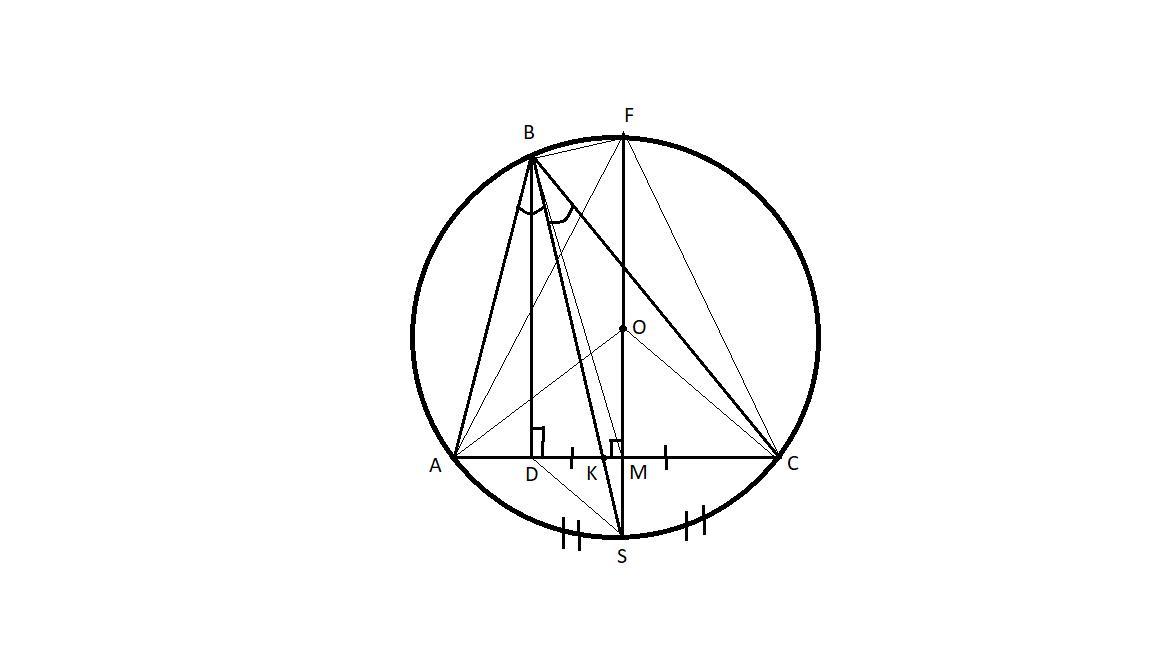
Рассмотрим неравнобедренный Δ ABC

Опишем около Δ ABC окружность .

Проведем  к стороне AC отрезок OM и продлим его до диаметра окружности FS.

Δ AOC - равнобедренный, поскольку OA = OС  как радиусы окружности.  Таким образом, его медиана OM (M делит AC пополам) является и его высотой, но тогда и медиана FM  треугольника AFC является его высотой, а значит он так же равнобедренный. Но тогда, эта высота является и биссектрисой, то есть ∠AFS =∠SFC, причем эти углы вписаны в окружность, а значит опираются на равные дуги.  Иначе говоря, дуга AS равна дуге SC, но тогда и вписанные углы ∠ABS = ∠SBC .  

Таким образом, BS биссектриса ∠B треугольника ABC ,  пусть она пересекает сторону AC в точке K.

BD ║ FS как два перпендикуляра к одной прямой AC, то есть SDBF - трапеция, а  ЛЮБАЯ трапеция является выпуклым четырехугольником, причем BS ее диагональ. Теперь придется сослаться на одну аксиому, а именно, что все точки диагонали выпуклого четырехугольника лежат внутри четырехугольника, но тогда и точка K лежит внутри трапеции (K∈SDBF).

Геометрическое место точек, принадлежащих и трапеции и отрезку AC - это отрезок DM.

Таким образом, раз точка K∈AC и K∈ SDBF , то K∈DM

Что и требовалось доказать.