Предмет: Математика,
автор: JackDanie1s
Помогите с решением, нужно найти область определения и решить неравенство
Приложения:
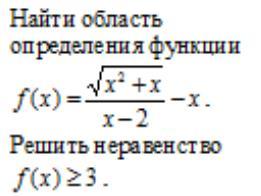
mmb1:
откуда такое?
Видно, что не из печатного издания...
Ответы
Автор ответа:
1
1.Область определения:
О т в е т. (-∞;-1] U[0; 2) U (2; +∞)
2.
Если x > 2, ( см ОДЗ x ∈(2;+∞),
то
Пусть
⇒
⇒
⇒
⇒
D=1+36=37
C учетом x >2 получаем
Если x < 2, ( см ОДЗ: x ∈(-∞;-1] U[0; 2) )
⇒
или
C учетом ОДЗ: x ∈(-∞;-1] U[0; 2) получаем
Объединяем оба полученных ответа
О т в е т.
Уважаемые модераторы, антиспамеры и другие, увлекающиеся отметкой нарушений. Решение пишется не для ВАС. Дайте возможность задавшему вопрос, посмотреть на мои рассуждения!. И только по согласованию с решающим удаляйте. А для н чала сами попробуйте решить....
Вот теперь задавший вопрос смотрел решение. Удаляйте...
решение уравнения:http://prntscr.com/to6qov
О т в е т. (-∞; x₁] U (2;x₂];x₁=(-1-sqrt(37))/2;x₂=(-1+sqrt(37))/2
Опечатка,,,
Похожие вопросы
Предмет: Английский язык,
автор: dashutaborodin
Предмет: Русский язык,
автор: Голубочка
Предмет: Русский язык,
автор: dinadina09smir
Предмет: Физика,
автор: katyakaterina2004
Предмет: Геометрия,
автор: gordienko94