Question

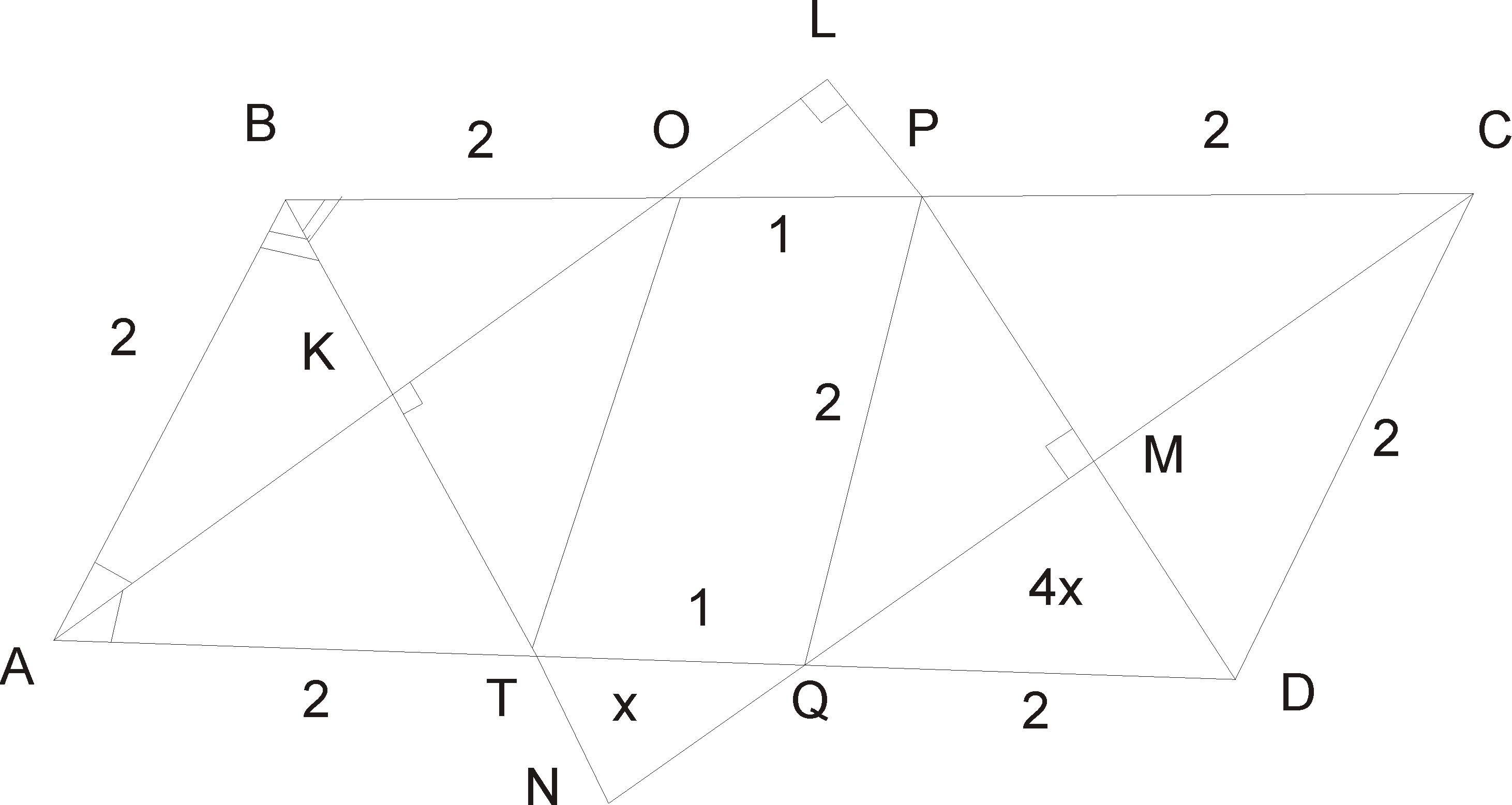
В параллелограмме ABCD со сторонами АВ = 2 и AD = 5 биссектриса угла А пересекает биссектрисы углов В и D в точках К L соответственно, а биссектри­са угла, С пересекает те же биссектрисы в точках N и М соответственно. Най­дите отношение площади четырехугольника KLMN к площади параллело­грамма ABCD Варианты ответа:

Answer 1

Ответ:

9/20

Пошаговое объяснение:

треугольники АВК КВО АТ ТКО равны между собой

треуг PMC CMD DMQ QPM равны между собой

тк угол А=С а угол В=D то все эти 8 треуг равны

площади подобных треуг относятся как квадраты сторон

QD/TQ=2/1

S(QMD)/S(TQN)=4/1

Если обозначить S(АВК) за х то S(TQN)=x/4

S(ABCD)=10x

S(OPQT)=S(BOTA)/2

S(KLMN)=4,5 x