Question

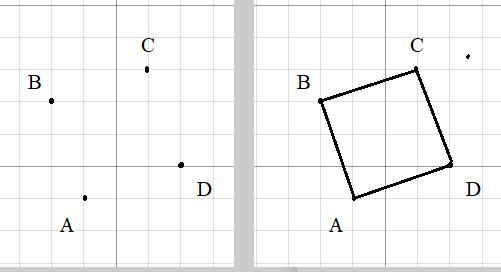
Найти площадь четырехугольника, вершины которого расположены в точках A(4;4), B(3;7), C(6;8), D(7;5).

Answer 1

Ответ:

Пошаговое объяснение:

АВ=√((3-4)²+(7-4)²)=√(1+9)=√10

АD=√((7-4)²+(5-4)²)=√(1+9)=√10

DC=√((-1)²+3²)=√10

ВС=√(3²+1²)=√10

AD*AB=(3;1)*(-1;3)=-3+3=0⇒∠А=90°

АВСD- квадрат. Его площадь равна (√10)²=10

Answer 2

$\vec {AD}=\vec {BC}$

$\vec {BC}=(6-3;8-7)=(3;1)$

⇒

$\vec {AD}=\vec {BC}$  ( значит векторы сонаправлены и их длины равны)

$|\vec {AD}|=|\vec {BC}|=\sqrt{3^2+1^2}=\sqrt{10}$

Векторы сонаправлены, значит прямые AD и BC параллельны

$\vec {AB}=(3-4;7-4)=(-1;3)$

$\vec {DC}=(6-7;8-5)=(-1;3)$

$\vec {AB}=\vec {DC}$

$|\vec {AB}|=|\vec {DC}|=\sqrt{(-1)^2+3^2}=\sqrt{10}$

Противоположные стороны четырехугольника параллельны

Четырехугольник параллелограмм

Все стороны параллелограмма   равны

Этот четырехугольник ромб.

Так как скалярное произведение векторов

$\vec {AD}\cdot\vec {AB}=3\cdot (-1)+1\cdot 3=0$

$\vec {AD}$  ⊥  $\vec {AB}$

Значит ABCD - квадрат

S( квадрата)=(√10)²=10  кв. ед