Question

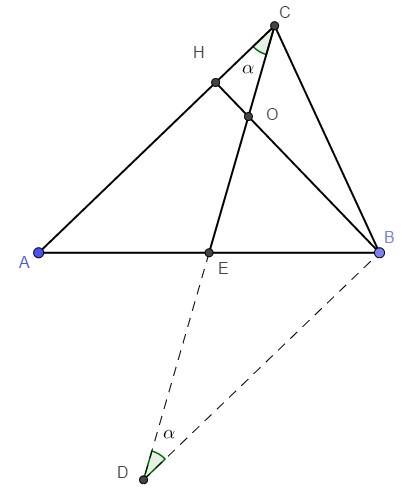
В треугольнике ABC высота BH и медиана СЕ пересекаются в точке O. Известно, расстояние что BO=4; OH=1; CE=5. Найдите сторону АВ. P.S. Решить без теореме Менелая и всяких готовых формул медиан.

Answer 1

Продлим $CE$ до пересечения прямой $BD\parallel AC$. Треугольники $DEB$ и $AEC$ равны по стороне и двум прилежащим углам (т.к. СЕ - медиана, то AE = EB и ∠CEA = ∠DEB как вертикальные; ∠ACE = ∠BDE как накрест лежащие). Из подобия треугольников $DOB$ и $COH$ (по двум углам) следует пропорциональность соответствующих сторон.

$\dfrac{BO}{OH}=\dfrac{BD}{CH}=\dfrac{DO}{CO}\Rightarrow~\dfrac{4}{1}=\dfrac{5-CO+5}{CO}\Rightarrow CO=2~ and~ AB=BD=4CH$

Пусть $\angle HCO=\angle ODB=\alpha$, тогда по теореме косинусов :

$OH^2=CH^2+CO^2-2CH\cdot CO\cos \alpha\\ OB^2=DO^2+BD^2-2DO\cdot BD\cos\alpha$

$1^2=CH^2+2^2-4CH\cos \alpha\\ 4^2=8^2+16CH^2-8\cdot 8CH\cos \alpha$

От второго равенства отнимем первое, умноженное на 16

$4^2-1^2=8^2-CH^2+16CH^2-2^2\\ \\ CH^2=3$

$CH=\sqrt{3}$

Тогда $\cos \alpha=\dfrac{1-3-4}{-4\sqrt{3}}=\dfrac{\sqrt{3}}{2}$. По теореме косинусов для ΔDEB:

$BE^2=BD^2+DE^2-2BD\cdot DE\cos \alpha=5^2+\big(4\sqrt{3}\big)^2-2\cdot 5\cdot 4\sqrt{3}\cdot \dfrac{\sqrt{3}}{2}=13$

$BE=\sqrt{13}$ отсюда $AB=2BE=2\sqrt{13}.$

Ответ: 2√13

Answer 2

Ответ:

2√13  без Менелая и всяких готовых формул медиан

Объяснение: