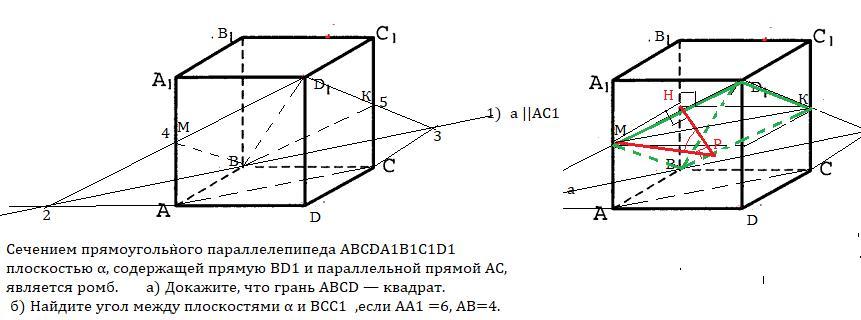
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1
плоскостью α, содержащей прямую BD1 и параллельной прямой AC,
является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями α и BCC1
, если AA1 =6, AB=4.
(108/145)
ЕГЭ 2019. Математика
Геометрия. Стереометрия
Задача 14 (профильный уровень)
Под редакцией И. В. Ященко
Ответы
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1
плоскостью α, содержащей прямую BD1 и параллельной прямой AC,
является ромб. а) Докажите, что грань ABCD — квадрат. б) Найдите угол между плоскостями α и BCC1 , если AA1 =6, AB=4.
Объяснение:
а) Проведем а||АС, значит а параллельна диагональному сечению АСС₁А₁⇒ МК||АС.
По условию BMD₁К-ромб, значит D₁В⊥МК по свойству диагоналей ромба и МК||АС. Тогда по т. о 3-х перпендикулярах : если наклонная D₁В перпендикулярна прямой лежащей в плоскости АС , то и проекция DВ⊥АС ( прямой , лежащей в плоскости ). Получили , что в прямоугольнике АВСD диагонали АС⊥DВ ⇒ АВСD -квадрат.
б)Проведем через М и К ( середины ребер) плоскость β║(АВС) , получим точку Н на ребре ВВ₁ , ВН=НВ₁=3 .
Пусть НР⊥ВК, т.к. МН⊥ВВ₁ ⇒ МР⊥ВК по т. о трех перпендикулярах⇒∠МРН-линейный угол данного двугранного.
ΔВНК -прямоугольный, ВК=√(16+9)=5.
ΔВНР≈ΔВНК ( по 2 углам общему и прямому) , значит сходственные стороны пропорциональны :
НР:НВ=НК:ВК , НР:3=4:5 , НР=12/5.
ΔМНР -прямоугольный , tg∠МРН=МН:РН , tg∠МРН=20/12=5/3
∠МРН=аrctg(5/3).
Эту задачу можно решить методом аналитической геометрии.
Расположим заданный параллелепипед в прямоугольной системе координат точкой В в начале, ВА по оси Ох ВС по оси Оу.
Сечение пересекает боковые рёбра АА1 и СС1 посредине в точках М и К.
Координаты точек для плоскости ВКД1:
В(0; 0; 0), К(0; 4; 3) и Д1(4; 4; 6).
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x - 0 y - 0 z - 0
0 - 0 4 - 0 3 - 0
4 - 0 4 - 0 6 - 0 = 0
x - 0 y - 0 z - 0
0 4 3
4 4 6 = 0
(x - 0) (4·6-3·4) - (y - 0) (0·6-3·4) + (z - 0) (0·4-4·4) = 0
12 x - 0 + 12 y - 0 + (-16) z - 0 = 0
12x + 12y - 16z = 0 или, сократив на 4:
3x + 3y - 4z = 0 .
Плоскость BCC1 - это плоскость zOy, её уравнение х = 0.
Угол между плоскостями определяется по формуле:
cos α = |A1·A2 + B1·B2 + C1·C2|
√(A1² + B1² + C1²) √(A2² + B2² + C2²).
Подставим значения:
cos α = |3·1 + 3·0 + (-4)·0|
√(3² + 3² + (-4)²) √(1² + 0² + 0²).
Получаем cos α = 3/√34 = 3√34/34.
Угол α = arc cos(3√34/34) = 59,036°.