Предмет: Физика,
автор: mininstepan1
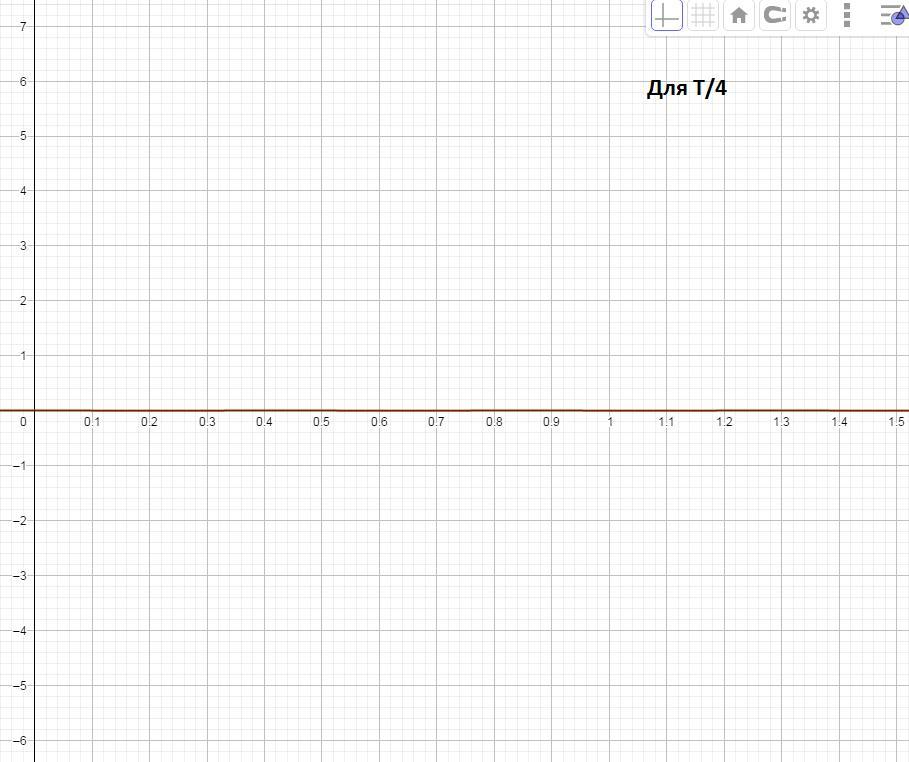
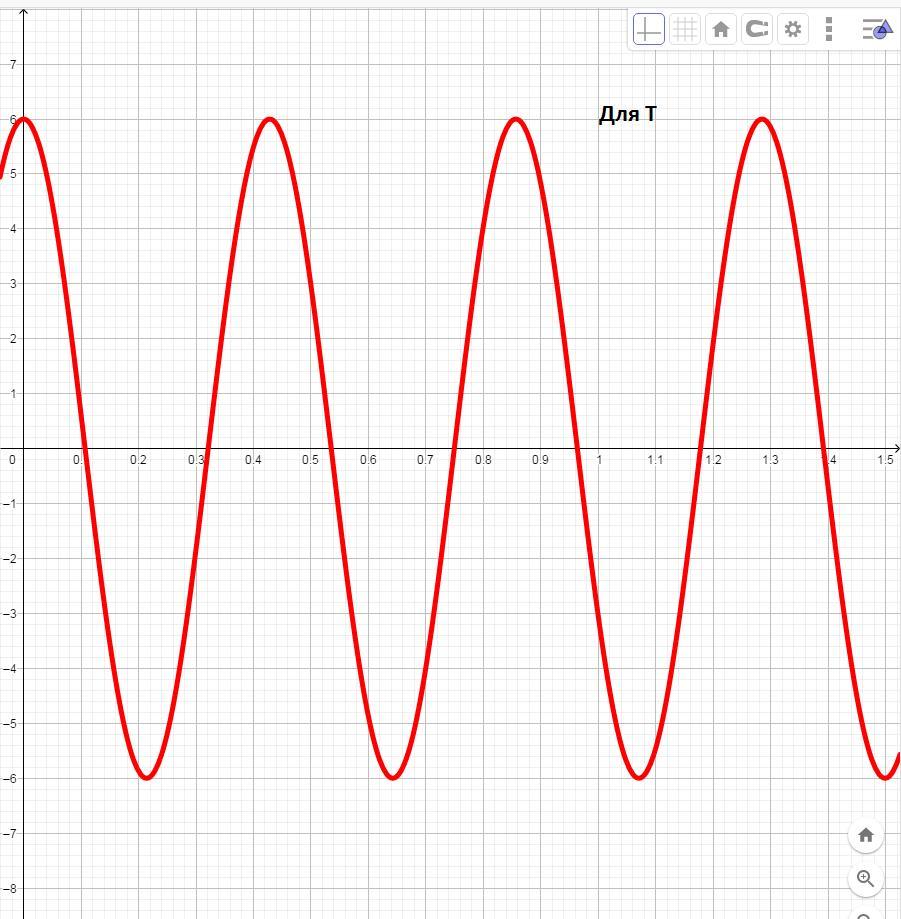
*ЗАДАЧА * Медный стержень длиной l=1.5м закреплен с одного конца, на котором расположен источник продольных колебаний с частотой =8675 гц. Источник возбуждает в стержне бегущую волну е(x, t) =3cos (amegat-kx), мкм.плотность меди p=8900 модуль упругости Е=123Гпа.Получить уравнение стоячей волны., возниквющей в результате наложения бегущей и отраженной от противоположного свободного конца стержня. Определить длину стоячий волны, амплитуду, а так же расположение узлов и пучностей на длине стержня. Изобразить графический возникающую волну для моментов времени t1=T/4 и t2=T
Leon8634:
Не совсем ясно условие закрепления конца стержня, на котором стоит источник колебаний, если его закрепить наглухо, то источник не возбудит в стержне бегущей волны, поэтому решил задачу с позиции, что источник все же подвижен.
Ответы
Автор ответа:
2
Ответ:
Прежде всего найдем скорость продольной волны
м/с
Циклическая частота
рад/с
Волновое число
1/м
Тогда уравнение бегущей волны примет вид
Эта волна распространяется в прямом направлении. В свободном конце должна быть пучность смещения. От свободного конца волна должна отразиться в фазе (для того, чтобы возникла пучность). Значит уравнение отраженной волны имеет вид
Их сумма и даст уравнение стоячей волны
Длина стоячей волны равна половине длины бегущей волны
м
Амплитуда стоячей волны равна удвоенной амплитуде бегущей, т.е. 6 мкм
Узлы
На длине стержня узлы будут в точках 0,105; 0,315; 0,525; 0,735; 0,945; 1,155; 1,365 метров
Пучности
Их координаты 0; 0,21; 0,42; 0,63; 0,84; 1,05; 1,26; 1,5 метра
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: арнет
Предмет: Английский язык,
автор: 89099772862
Предмет: Русский язык,
автор: Ирина4875
Предмет: Литература,
автор: IDEA31
Предмет: Биология,
автор: ординат