Предмет: Геометрия,
автор: Scvaps
В правильной четырехугольной пирамиде боковое ребро образует с плоскостью основание угол 45. Площадь его диагонального сечения равна 9 см. Найти объем пирамиды. Решите пожалуйста
Ответы
Автор ответа:
0
Ответ:на фотографии
Объяснение:
Приложения:
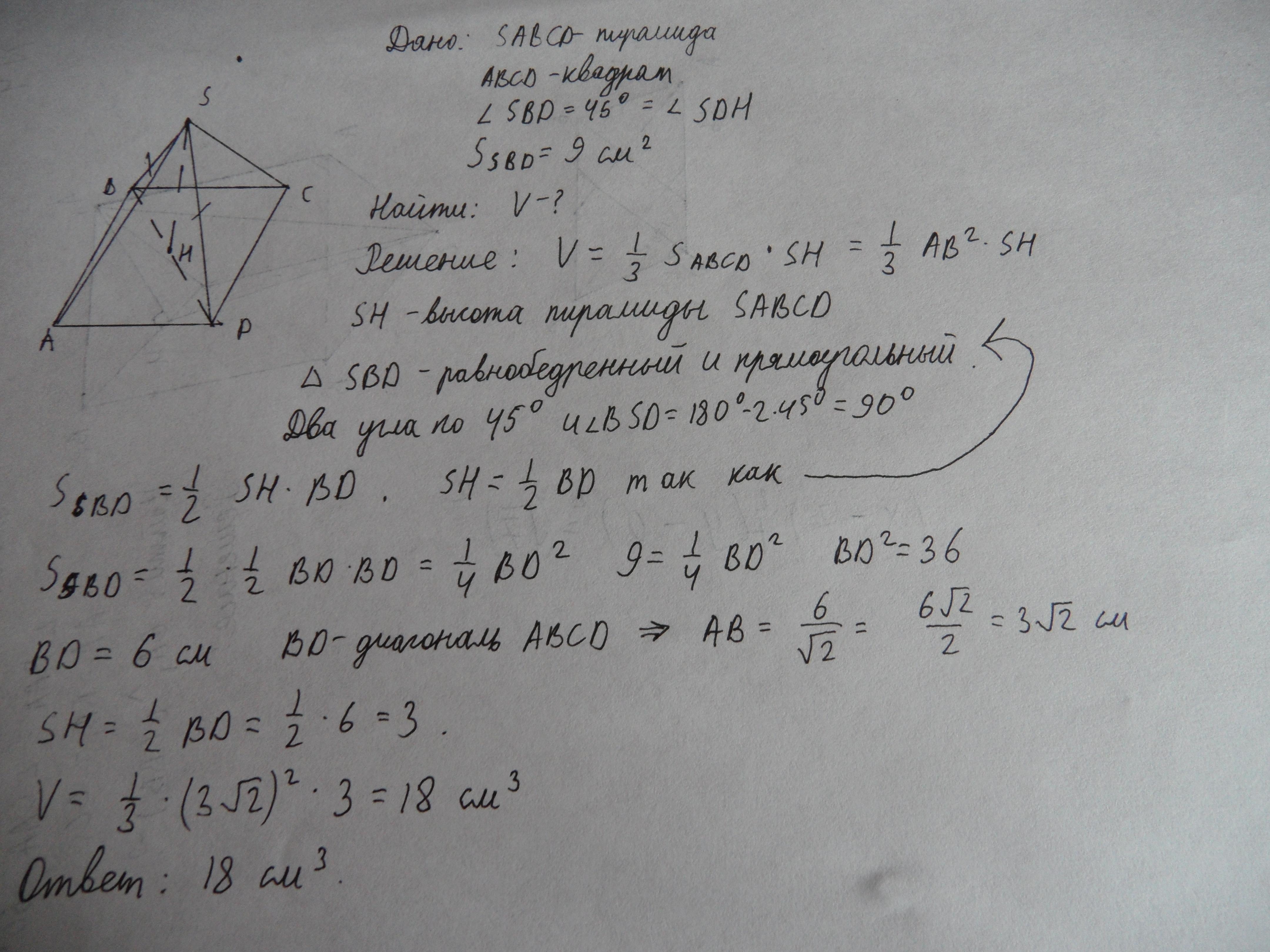
Автор ответа:
0
Диагональное сечение пирамиды- равнобедренный треугольник, углы при основании которого 45° по условию, значит, угол при вершине 180°-2*45°=90°, высота, проведенная к основанию в этом треугольнике равна половине основания, а площадь равна половине основания на высоту, значит, квадрат высоты равен 9 см², высота 3 см, она же и высота пирамиды, теперь легко вычислить объем пирамиды по формуле v=(1/3)*s*h, где s- площадь основания, т.е. квадрата, она равна половине произведения диагоналей, т.е. (2*3)²/2; h-высота, равная 3 см, объем равен
(1/3)*36*3/2=18/см²/
Похожие вопросы
Предмет: Русский язык,
автор: marinagrigorya
Предмет: Русский язык,
автор: matveikakimyaev
Предмет: Английский язык,
автор: куукуська94
Предмет: Литература,
автор: DeadUser