Найдите все значения параметра b при которых система имеет единственное решение
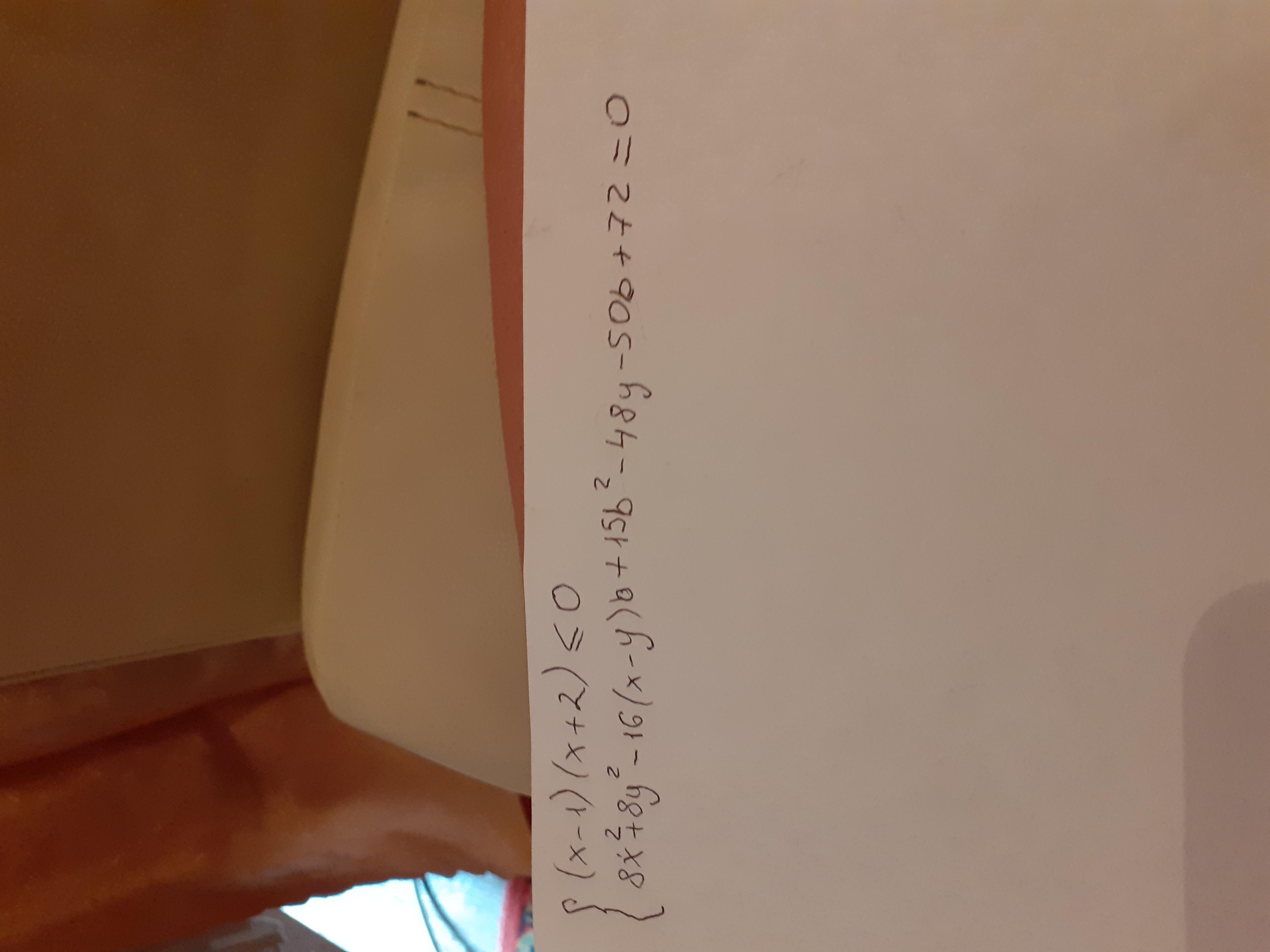
Ответы
Ответ:
При этих значениях b₁=0, b₂=-2 система неравенств имеет единственное решение.
Пошаговое объяснение:
Соберем полный квадрат из первого уравнения
(8x²-16xb)+8y²+16yb+15b²-48y-50b+72=0
8(x²-2xb+b²)-8b²+8y²+16yb+15b²-48y-50b+72=0
Приводим подобные по b².
8(x-b)²+8y²+16yb+7b²-48y-50b+72=0
Собираем новый квадрат
8(x-b)²+8(y²+2yb-6у)+7b²-50b+72=0
8(x-b)²+8(y+(b-3))²-8(b-3)²+7b²-50b+72=0
8(x-b)²+8(y+(b-3))²-8b²+48b-72+7b²-50b+72=0
8(x-b)²+8(y+(b-3))²-b²-2b=0
8(x-b)²+8(y+(b-3))²=b²+2b (*)
Если правая часть равна нулю, то слева скобки каждая по отдельности должны быть равны 0.
Правая часть равна нулю, когда b²+2b=0
b(b+2)=0
b₁=0, b₂=-2.
1) Если b₁=0, то (*) принимает вид
8x²+8(y-3)²=0
Это возможно, когда х=0 и у=-3.
Если подставить х=0 в первое неравенство системы, то получим
(0-1)(0+2)≤0
-1*2≤0
-2≤0 - выполняется. То есть при b₁=0 система имеет единственное решение.
2) Если b₂=-2, то (*) принимает вид
8(x+2)²+8(y-5)²=0
При х=-2 и у=5 будет единственное решение данного уравнения.
Подставим х=-2 в первое уравнение системы
(-2-1)(-2+2)≤0
-3*0≤0
0≤0 - выполняется. То есть при b₂=-2 система имеет единственное решение.