Question

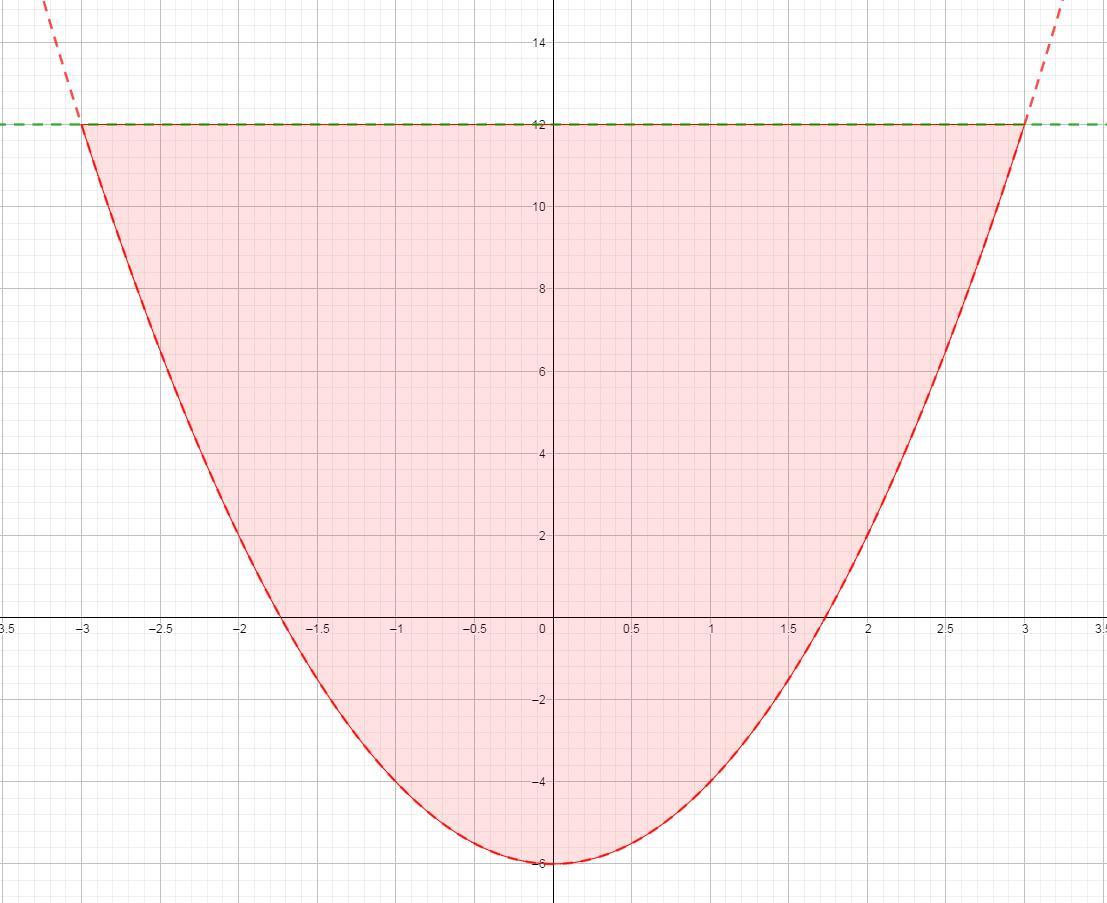
Вычислите площадь фигуры, ограниченной параболой y = 2x^2-6 и линией y=12. Ответ 72, но как это решается?

Answer 1

Ответ:

72

Пошаговое объяснение:

Для начала найдем абсциссы точек пересечения графиков функций

$2x^2-6=12 => 2x^2=18 => x^2=9=> x=\pm 3$

Площадь найдем как разность площадей под верхним и нижним графиком, проще говоря как разность соответствующих определенных интегралов

$S=\int\limits^3_{-3} {12} \, dx- \int\limits^3_{-3} {(2x^2-6)} \, dx=\int\limits^3_{-3} {(12-2x^2+6)} \, dx= \int\limits^3_{-3} {(18-2x^2)} \, dx=$

$=(18x-\frac{2}{3}x^3)|_{-3}^3=18*3-\frac{2}{3}*3^3-(18*(-3)-\frac{2}{3}(-3)^3 )=72$.