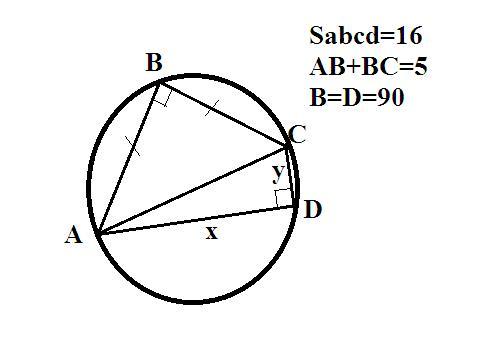
В четырёхугольнике ABCD: AB=BC=5, ∠ABC=∠ADC=90∘, AD>CD. Известно, что площадь четырёхугольника равна 16. Найдите длину отрезка AD.
Ответы
Ответ:
Объяснение:
Данный четырехугольник состоит из двух прямоугольных треугольников с общей гипотенузой АС и вписан в окружность (сумма противоположных углов равна 180°).
Площадь треугольника АВС=5*5/2=12,5 ед².
Площадь треугольника ACD=16-12,5=3,5 ед²
АС=√(5²+5²)=√50.
Обозначим AD - x, CD - y;
составляем систему уравнений:
ху/2=3,5
х²+у²=(√50)².
решая систему находим х=AD=7 ед, у=CD=1 ед.
Ответ: 1(ед), 7(ед)
Объяснение: Рассмотрим ∆АВС. Он прямоугольный где АВ и ВС - катеты, а АС - гипотенуза. ∆АВС равнобедренный, а в равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому АС=5√2. Найдём площадь ∆АВС по формуле: S=½×AB×BC=½×5²=½×25=12,5(ед²)
Если площадь ∆АВС=12,5(ед²), то площадь ∆АСД=16-12,5=3,5(ед²)
Рассмотрим ∆АСД. Он прямоугольный где АД и СД- катеты а АС гипотенуза. Пусть АД=х, а СД=у. Площадь ∆АСД также вычисляется по формуле:
S=½×АД×СД, тогда: ½×х×у=3,5. Составим второе уравнение используя теорему Пифагора: х²+у²=(5√2)². Решим систему уравнений:
½×ху=3,5
х²+у²=(5√2)
х=3,5÷½÷у
х²+у²=25×2
х=3,5×2÷у
х²+у²=50
х=7/у
х²+у²=50
Подставим значение х во второе уравнение:
(7/у)²+у²=50
49/у²+у²=50 |находим общий знаменатель и получим:
(49+у⁴)/у²=50 |перемножим числитель и знаменатель соседних дробей между собой крест накрест:
49+у⁴=50у²
у⁴-50у²+49=0 | пусть у²=у, тогда:
у²-50у+49=0
Д=2500-4×49=2500-196=2304
у1=(50-48)/2=2/2=1
у2=(50+48)/2=98/2=49
Итак: мы нашли 2 значения у, но нам не подходит значение у2=49, поскольку площадь четырёхугольника намного меньше, поэтому мы используем у1=1
Теперь подставим значение у в уравнение: х=7/у=7/1=7
Итак: одна сторона=1ед, вторая=7ед
Ѕ(АСD)=Ѕ(ABCD)-S(ABC)=16-12,5=3,5
S(ACD)=AD•CD/2=> AD•CD=7
В ∆ АСD примем АD=b, тогда СD=7/b
По т.Пифагора AC²=b²-(7/b)², откуда
50=b²+49/b² =>
b⁴-50b²+49=0
Пусть b²=х
Тогда уравнение примет вид
х²-50х+49=0
Решив квадратное уравнение, находим х₁=49, х₂=1 ( не подходит, т.к. по условию АD>CD)
b²=[1=49, b=√49=7
AD=7 (ед. длины)