Предмет: Геометрия,
автор: Аноним
HELP ME!!!!!! РЕБЯТА две вершины правильного треугольника лежат на оси абцисс, а третья - на оси ординат. Найдите длину стороны треугольника если сумма всех координат всех его вершин равна 2 под корнем 3
Ответы
Автор ответа:
2
Ответ: а=4 .
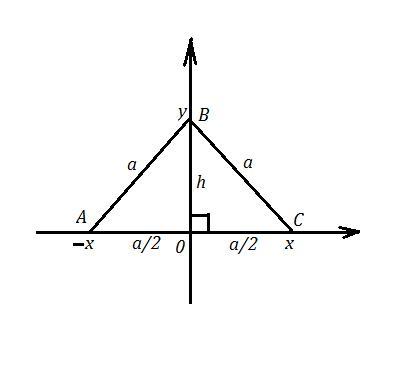
ΔАВС - правильный ⇒ все его стороны равны "а" . Высота равностороннего треугольника является и медианой. Так как ОХ⊥ОУ , то если две вершины лежат на оси ОХ, тогда третья вершина лежит на оси ОУ. Пусть вершины А и С лежат на оси ОХ, тогда координаты точки А(х,0) , а координаты точки С(-х,0). Вершина В лежит на оси ОУ и её координаты будут В(0,у) .
По условию сумма всех координат равна:
(-х+0)+(х+0)+(0+у)=2√3 ⇒
у=2√3 (2√3>0 ⇒ точка В лежит в верхней полуплоскости) ⇒ высота ВО=h=2√3 .
По теореме Пифагора из прямоугольного ΔАВО имеем:
Длина сторона правильного треугольника равна 4 .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: smekalin87
Предмет: Українська мова,
автор: martselyuklesya
Предмет: Русский язык,
автор: солнце222
Предмет: Биология,
автор: Анна15062004