Найти все значения параметра а, при каждом из которых уравнение не имеет положительных корней
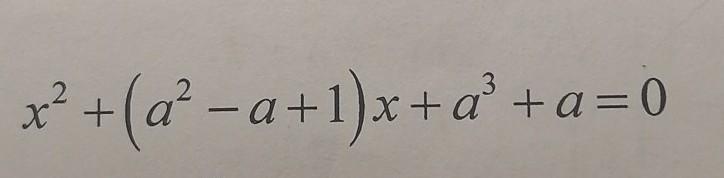
Ответы
Ответ:
Пошаговое объяснение:
Рассмотрим 2 случая:
1-й случай: .
Заметим, что тогда дискриминант больше 0
так как
Значит уравнение имеет вещественные корни
По теореме Виета:
, значит
-- разных знаков, то есть лежат по разные стороны от нуля. Что не удовлетваряет требованиям задачи. Значит никакие
не подходят.
2-й случай:
Рассмотрим 2 подслучая:
2.1) оказалось, что дискриминант .
Тогда уравнение не имеет положительных корней (потому что оно не имеет вещественных корней).
2.2) оказалось, что Тогда уравнение имеет корни (возможно, кратные). Обозначим их
. Заметим, что эти корни одного знака, так как их произведение (по теореме Виета):
. То есть они лежат по одну сторону от нуля. Чтобы понять по какую сторону от 0 они лежат, посмотрим на их сумму и опять воспользуемся теоремой Виета:
, значит оба корня
.
Это значит, что все подходят.