Question

у трикутнику медіана проведена до сторони утворює з нею кут 120°. дві інші сторони дорівнюють 14 і 2✓19. знайдіть сторону.
пожааалуйста​

Answer 1

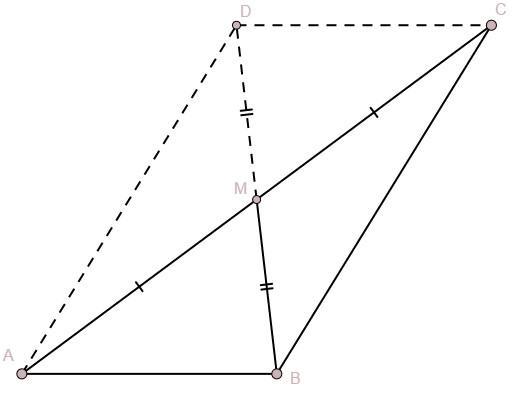
Против большего угла лежит большая сторона. Обозначим $AB=2\sqrt{19},~ BC=14.$ Поскольку $BM$ — медиана, то $AM=MC=\dfrac{AC}{2}$. Достроим до параллелограмма $ABCD$. Воспользуемся свойством: сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

$2(AB^2+BC^2)=BD^2+AC^2$

$BD^2+AC^2=2\cdot \Big((2\sqrt{19})^2+14^2\Big)=544$

По теореме Косинусов из треугольника $BMC$ :

$BC^2=MB^2+MC^2-2MB\cdot MC\cdot \cos 120^\circ \\ \\ 14^2=\left(\dfrac{BD}{2}\right)^2+\left(\dfrac{AC}{2}\right)^2-2\cdot \dfrac{BD}{2}\cdot \dfrac{AC}{2}\cdot \left(-\dfrac{1}{2}\right)\\ \\ 14^2\cdot 4=BD^2+AC^2+BD\cdot AC$

$14^2\cdot 4=544+BD\cdot AC\\ \\ BD\cdot AC=240~~\Rightarrow~~ BD=\dfrac{240}{AC}$

Далее подставляем BD в то выражение, где было использовано свойство, мы имеем:

$\left(\dfrac{240}{AC}\right)^2+AC^2=544\\ \\ \dfrac{240^2}{AC^2}+AC^2-544=0$

Пусть $AC^2=t$ при этом $t>0$, получим

$\dfrac{240^2}{t}+t-544=0~~~\Big|\cdot t\ne 0\\ \\ t^2-544t+240^2=0\\ \\ D=(-544)^2-4\cdot 1\cdot 240^2=65536;~~\sqrt{D}=256$

$t_1=\dfrac{544-256}{2\cdot 1}=144;~~~~~~~~~ t_2=\dfrac{544+256}{2\cdot 1}=400$

Теперь выполним обратную замену

$AC^2=144~~~\Rightarrow~~~ AC=12\\ \\ AC^2=400~~~\Rightarrow~~~ AC=20$

Ответ: 12 или 20.