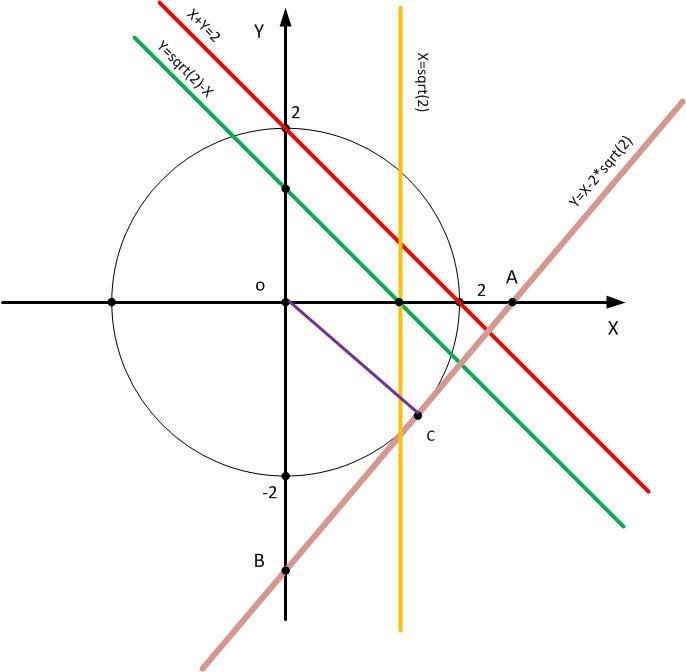
Какая из прямых является касательной к окружности  a)x+y=2 b) y=x-2√2 c)x=√2 d)y=√2 - x
a)x+y=2 b) y=x-2√2 c)x=√2 d)y=√2 - x
Ответы
Пошаговое объяснение:
Так, радиус мы знаем (x²+y²=r²), и он равен √4=2
По «свободным коэффициентам» x и y мы видим, что окружность является окружностью, и центром является начало координат.
Нарисуем окружность, и попробуем подобрать все линейные уравнения, которые нам даны: (см рисунок)
По рисунку видно, что касательная данной окружности является пункт под номером
b) y=x-2√2

Ответ:
Пошаговое объяснение:
а. График x+y=2 (красный на чертеже) не есть касательная, а есть секущая окружности. Пересекается с окружностью в т:
x=0; y=2 и y=0; x=2.
с. График функции x=√2 (желтый) - это вертикальная прямая, проходящая через точку с координатами x=√2; y=0. √2<2, поэтому этот график также секущая для окружности.
d. График функции y=√2-x (зеленый) проходит через точки с координатами:
x=0; y=√2 и y=0; x=√2
√2<2 поэтому и эта прямая есть секущая для окружности.
b. График функции y=x-2√2 (цвет, наверное, называется бежевый).
Этот график пересекается с осями оX и oY в точках А и В в точках А(2√2;0) и B(0;2√2) соответственно. Если этот график - касательная к окружности, то отрезок oC - перпендикулярен графику функции в точке касания (т.С), и расстояние l oC l = 2 т.е. радиусу окружности.
Проверим.
l oA l = l oB l, следовательно треугольник AoB -прямоугольный и равнобедренный. У такого треугольника углы у основания равны 45°.
Рассмотрим Δ oAC. Он также прямоугольный и равнобедренный (т.к. ∠ oCA - прямой, а ∠ oAC =45°).
l oC l=l oA l*cos 45°;
l oC l=2√2*cos45=2√2*√2/2=(√2)²=2
Задача решена! (это не факториал)